题目内容
19．一个几何体的三视图如图所示，若该几何体的体积为$\frac{10}{3}$，则a•b2的值为4．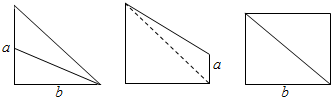
分析 由已知的三视图可得几何体的直观图，进而根据该几何体的体积为$\frac{10}{3}$，可得答案．
解答 解：由已知的三视图可得该几何体的直观图如下所示：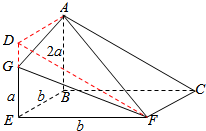
它是由三棱柱ABC-DEF切去一个三棱锥F-ADG所得的组合体，
故体积V=$\frac{1}{2}$×2ab×b-$\frac{1}{3}$×$\frac{1}{2}$（2a-a）b×b=$\frac{5}{6}$ab2=$\frac{10}{3}$，
∴ab2=4，
故答案为：4．
点评 本题考查的知识点是由三视图求体积和表面积，解决本题的关键是得到该几何体的形状．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
14．双曲线x2-y2=1右支上一点P（a，b）到直线l：y=x的距离d=$\sqrt{2}$．则a+b=（ ）
| A． | -$\frac{1}{2}$ | B． | $\frac{1}{2}$ | C． | $\frac{1}{2}$或-$\frac{1}{2}$ | D． | 2或-2 |