题目内容
8.已知数列{an}是公差不为零的等差数列,a1=2,且a2,a4,a8成等比数列.则数列{an}的通项公式为an=2n.分析 数列{an}是公差d≠0的等差数列,由a2,a4,a8成等比数列,可得${a}_{4}^{2}$=a2a8,利用等差数列通项公式代入解出d即可得出.
解答 解:数列{an}是公差d≠0的等差数列,
∵a2,a4,a8成等比数列,
∴${a}_{4}^{2}$=a2a8,
∴(2+3d)2=(2+d)(2+7d),
化为2d2-4d=0,
解得d=2或d=0(舍).
∴an=2+2(n-1)
=2n.
故答案为:an=2n.
点评 本题考查了等差数列与等比数列的通项公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
18.某四棱锥的三视图如图所示,则该四棱锥的体积是( )
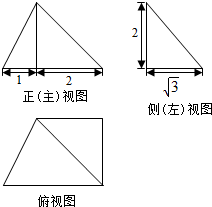

| A. | $5\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | $\frac{{5\sqrt{3}}}{3}$ | D. | $\frac{2\sqrt{3}}{3}$ |
16.方程x-lg$\frac{1}{x}$-3=0的解所在的区间为( )
| A. | (0,1) | B. | (1,2) | C. | (2,3) | D. | (3,+∞) |
17.“m>1”是“函数f(x)=m+log2x(x≥1)不存在零点”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
18.将函数y=cos2x的图象向右平移$\frac{π}{4}$个单位长度,得到函数y=f(x)•sin x的图象,则f(x)的表达式可以是( )
| A. | f(x)=-2cos x | B. | f(x)=2cos x | ||
| C. | f(x)=$\frac{\sqrt{2}}{2}$sin 2x | D. | f(x)=$\frac{\sqrt{2}}{2}$(sin 2x+cos 2x) |