��Ŀ����
����Ŀ����A�ǵ�λԲx2+y2=1�ϵ�����һ�㣬l�ǹ���A��x�ᴹֱ��ֱ�ߣ�D��ֱ��l��x��Ľ��㣬��M��ֱ��l�ϣ�������حDMح=mحDAح��m��0����m��1��������A��Բ���˶�ʱ���ǵ�M�Ĺ켣Ϊ����C��
��I��������C�ķ��̣��ж�����CΪ����Բ���ߣ��������ꣻ
����ԭ����б��Ϊk��ֱ�߽�����C��P��Q���㣬����P�ڵ�һ���ޣ�����y���ϵ���ӰΪ��N��ֱ��QN������C����һ��H���Ƿ����m��ʹ�ö������k��0������PQ��PH�������ڣ���m��ֵ���������ڣ���˵�����ɣ�
���𰸡��⣺��I����ͼ1����M��x��y����A��x0 �� y0��
��حDMح=mحDAح����x=x0 �� |y|=m|y0|
��x0=x��|y0|= ![]() |y|��
|y|��
�ߵ�A��Բ���˶����� ![]() ��
��
�ٴ���ڼ�����������C�ķ���Ϊ ![]()
��m�ʣ�0��1���ȣ�1��+�ޣ���
��0��m��1ʱ������C�ǽ�����x���ϵ���Բ������������ֱ�Ϊ�� ![]() ����
���� ![]()
m��1ʱ������C�ǽ�����y���ϵ���Բ������������ֱ�Ϊ�� ![]() ����
���� ![]()
������ͼ2��3��x1�ʣ�0��1������P��x1 �� y1����H��x2 �� y2������Q����x1 �� ��y1����N��0��y1����
��P��H��������ԲC�ϣ��� 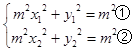
�٩��ڿɵ� ![]() ��
��
��Q��N��H���㹲�ߣ���kQN=kQH �� �� ![]()
��kPQkPH= ![]()
��PQ��PH����kPQkPH=��1
�� ![]()
��m��0���� ![]()
�ʴ��� ![]() ��ʹ�������Ӧ����Բ
��ʹ�������Ӧ����Բ ![]() �ϣ�������k��0������PQ��PH
�ϣ�������k��0������PQ��PH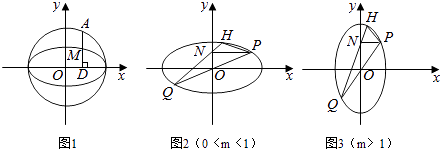
����������I����M��x��y����A��x0 �� y0��������حDMح=mحDAح��ȷ������֮��Ĺ�ϵx0=x��|y0|= ![]() |y|�����õ�A��Բ���˶�������������C�ķ��̣�����m�ʣ�0��1���ȣ�1��+�ޣ����������ۣ���ȷ���������ꣻ����x1�ʣ�0��1������P��x1 �� y1����H��x2 �� y2������Q����x1 �� ��y1����N��0��y1��������P��H��������ԲC�ϣ��ɵ�
|y|�����õ�A��Բ���˶�������������C�ķ��̣�����m�ʣ�0��1���ȣ�1��+�ޣ����������ۣ���ȷ���������ꣻ����x1�ʣ�0��1������P��x1 �� y1����H��x2 �� y2������Q����x1 �� ��y1����N��0��y1��������P��H��������ԲC�ϣ��ɵ� ![]() ���Ӷ��ɵÿɵ�
���Ӷ��ɵÿɵ� ![]() ������Q��N��H���㹲�ߣ���PQ��PH��������ý��ۣ�
������Q��N��H���㹲�ߣ���PQ��PH��������ý��ۣ�

 ���Ǽ���С����ϵ�д�
���Ǽ���С����ϵ�д� �Ͻ�ƽ���Ȿϵ�д�
�Ͻ�ƽ���Ȿϵ�д�