题目内容
7.平行六面体ABCD-A1B1C1D1中,∠A1AD=∠A1AB=60°,DAB=90°,A1A=3,AB=2,AD=1,则其对角线AC1的长为$\sqrt{23}$.分析 直接利用后利用平面向量的数量积进行运算.
解答 解:如图,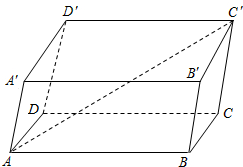
可得$\overrightarrow{AC′}=\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CC′}$=$\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{AA′}$,
故$|\overrightarrow{AC′}{|}^{2}=(\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{AA′})^{2}$=$|\overrightarrow{AB}{|}^{2}+|\overrightarrow{AD}{|}^{2}+|\overrightarrow{AA′}{|}^{2}$$+2(\overrightarrow{AB}•\overrightarrow{AD}+\overrightarrow{AB}•\overrightarrow{AA′}+\overrightarrow{AD}•\overrightarrow{AA′})$
=22+12+32+2(2×1×0+2×3×$\frac{1}{2}$+1×3×$\frac{1}{2}$)=23.
∴AC′=$\sqrt{23}$.
故答案为:$\sqrt{23}$.
点评 本题考查了利用平面向量求解立体几何问题,考查了平面向量的数量积运算,是基础的计算题.

练习册系列答案
相关题目
17.在△ABC中,AB=AC=5,BC=6,PA⊥平面ABC,PA=8,则P到BC的距离是( )
| A. | $\sqrt{5}$ | B. | $4\sqrt{5}$ | C. | $3\sqrt{5}$ | D. | $2\sqrt{5}$ |
18. 如图,正方体ABCD-A1B1C1D1中,O为底面ABCD的中心,M为棱BB1的中点,则下列结论中错误的是( )
如图,正方体ABCD-A1B1C1D1中,O为底面ABCD的中心,M为棱BB1的中点,则下列结论中错误的是( )
 如图,正方体ABCD-A1B1C1D1中,O为底面ABCD的中心,M为棱BB1的中点,则下列结论中错误的是( )
如图,正方体ABCD-A1B1C1D1中,O为底面ABCD的中心,M为棱BB1的中点,则下列结论中错误的是( )| A. | D1O∥平面A1BC1 | B. | D1O⊥平面AMC | ||
| C. | 异面直线BC1与AC所成的角等于60° | D. | 二面角M-AC-B等于45° |
2.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{3}}{2}$,过左焦点F的直线与椭圆相交于A、B两点,且有$\frac{1}{|AF|}$+$\frac{1}{|BF|}$=2,则椭圆的长半轴长a的值为( )
| A. | 2$\sqrt{3}$ | B. | 4 | C. | 3$\sqrt{2}$ | D. | 6 |
19.下图是导函数y=f′(x)的图象,则函数y=f(x)的极小值点为( )


| A. | a,x3,x6 | B. | x2 | C. | x3,x6 | D. | x4 |

 如图所示,为了开凿隧道,要测量隧道上D、E间的距离,为此在山的一侧选取适当点C,测得CA=400m,CB=600m,∠ACB=60°,又测得A、B两点到隧道口的距离AD=80m,BE=40m(A、D、E、B在一条直线上),计算隧道DE的长(精确到1m).
如图所示,为了开凿隧道,要测量隧道上D、E间的距离,为此在山的一侧选取适当点C,测得CA=400m,CB=600m,∠ACB=60°,又测得A、B两点到隧道口的距离AD=80m,BE=40m(A、D、E、B在一条直线上),计算隧道DE的长(精确到1m).