题目内容
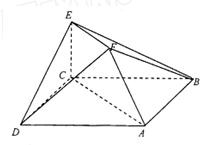
在如图所示的多面体中,底面△ABC是边长为2的正三角形,DA和EC均垂直于平面ABC,且DA=2,EC=1.
(1)求异面直线BE与AC所成角的余弦值;
(2)求二面角B-ED-A的正切值.
解:(1)取DA的中点F,连结FE、FB,则FE∥AC,
∴异面直线BE与AC所成的角等于∠BEF.
在△BEF中,FE=2,BF=BE=![]() ,∴cos∠BEF=
,∴cos∠BEF=![]() .
.
(2)由DA⊥平面ABC可知,DACB为直二面角,取AC的中点M,连结BM,则BM⊥AC,从而BM⊥平面ADEC,过点M作MN⊥直线DE,N为垂足,连结BN,则BN⊥直线DE.
因此,∠BNM是所求二面角的平面角.
设AC、DE的延长线相交于点P,∵DA=2EC,∴CP=2.
由△MNP≌△DAP,得![]() ,MP=3,DA=2,DP=2
,MP=3,DA=2,DP=2![]() ,于是MN=
,于是MN=![]() .
.
又BM=![]() ,从而tan∠BNM=
,从而tan∠BNM= .
.

练习册系列答案
相关题目
 在如图所示的多面体中,已知正方形ABCD和直角梯形ACEF所在的平面互相垂直,EC⊥AC,EF∥AC,AB=
在如图所示的多面体中,已知正方形ABCD和直角梯形ACEF所在的平面互相垂直,EC⊥AC,EF∥AC,AB=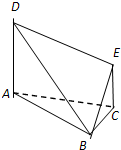 在如图所示的多面体中,底面△ABC是边长为2的正三角形,DA和EC均垂直于平面ABC,且DA=2,EC=1.
在如图所示的多面体中,底面△ABC是边长为2的正三角形,DA和EC均垂直于平面ABC,且DA=2,EC=1.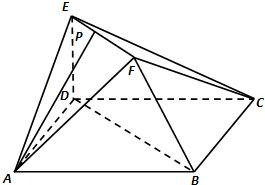 在如图所示的多面体中,已知正方形ABCD和
在如图所示的多面体中,已知正方形ABCD和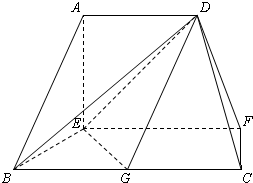 (2012•日照一模)在如图所示的多面体中,EF⊥平面AEB,AE⊥EB,AD∥EF,EF∥BC,BC=2AD=4,EF=3,AE=BE=2,G是BC的中点.
(2012•日照一模)在如图所示的多面体中,EF⊥平面AEB,AE⊥EB,AD∥EF,EF∥BC,BC=2AD=4,EF=3,AE=BE=2,G是BC的中点. 在如图所示的多面体中,AA1∥BB1,CC1⊥AC,CC1⊥BC.
在如图所示的多面体中,AA1∥BB1,CC1⊥AC,CC1⊥BC.