题目内容
【题目】如图,某景区内有两条道路![]() 、
、![]() ,现计划在
,现计划在![]() 上选择一点
上选择一点![]() ,新建道路
,新建道路![]() ,并把
,并把![]() 所在的区域改造成绿化区域.已知
所在的区域改造成绿化区域.已知![]() ,
,![]() ,
,![]() .若绿化区域
.若绿化区域![]() 改造成本为
改造成本为![]() 万元
万元![]() ,新建道路
,新建道路![]() 成本为
成本为![]() 万元
万元![]() .
.
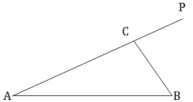
(1)①设![]() ,写出该计划所需总费用
,写出该计划所需总费用![]() 的表达式,并写出
的表达式,并写出![]() 的范围;
的范围;
②设![]() ,写出该计划所需总费用
,写出该计划所需总费用![]() 的表达式,并写出
的表达式,并写出![]() 的范围;
的范围;
(2)从上面两个函数关系中任选一个,求点![]() 在何处时改造计划的总费用最小.
在何处时改造计划的总费用最小.
【答案】(1)①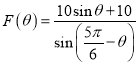 ,
,![]() ;②
;②![]() ;(2)
;(2)![]() .
.
【解析】
(1)①利用正弦定理求出![]() 、
、![]() 关于
关于![]() 的表达式,根据题意可得出
的表达式,根据题意可得出![]() 的表达式,并可求得
的表达式,并可求得![]() 的范围;
的范围;
②设![]() ,利用余弦定理求出
,利用余弦定理求出![]() ,根据题意可得出
,根据题意可得出![]() 的表达式,并可求得
的表达式,并可求得![]() 的取值范围;
的取值范围;
(2)利用导数求得函数![]() 的最小值,及其对应的
的最小值,及其对应的![]() 的值,进而得解.
的值,进而得解.
(1)①设![]() ,由正弦定理得
,由正弦定理得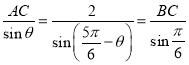 ,
,
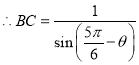 ,
,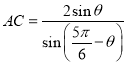 ,
,
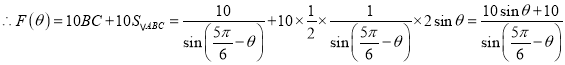 .
.
当点![]() 与点
与点![]() 重合的时候,
重合的时候,![]() ,所以
,所以![]() ;
;
②设![]() ,
,![]() ,
,
![]() ;
;
(2) ,则
,则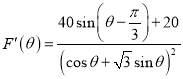 ,
,
令![]() ,得
,得![]() ,且
,且![]() ,所以
,所以![]() ,得
,得![]() .
.
当![]() 时,
时,![]() ,此时,函数
,此时,函数![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,此时,函数
,此时,函数![]() 单调递增.
单调递增.
所以当![]() ,即
,即![]() 时,改造计划的总费用最小.
时,改造计划的总费用最小.

 阅读快车系列答案
阅读快车系列答案【题目】根据调查,某学校开设了“街舞”、“围棋”、“武术”三个社团,三个社团参加的人数如下表所示:
社团 | 街舞 | 围棋 | 武术 |
人数 | 320 | 240 | 200 |
为调查社团开展情况,学校社团管理部采用分层抽样的方法从中抽取一个容量为n的样本,已知从“围棋”社团抽取的同学比从“街舞”社团抽取的同学少2人.
(1)求三个社团分别抽取了多少同学;
(2)若从“围棋”社团抽取的同学中选出2人担任该社团活动监督的职务,已知“围棋”社团被抽取的同学中有2名女生,求至少有1名女同学被选为监督职务的概率。
【题目】心理学家分析发现视觉和空间能力与性别有关,某数学兴趣小组为了验证这个结论,从兴趣小组中按分层抽样的方法抽取![]() 名同学(男
名同学(男![]() 女
女![]() ),给所有同学几何题和代数题各一题,让各位同学自由选择一道题进行解答.选题情况如下表:(单位:人)
),给所有同学几何题和代数题各一题,让各位同学自由选择一道题进行解答.选题情况如下表:(单位:人)
几何题 | 代数题 | 总计 | |
男同学 |
|
|
|
女同学 |
|
|
|
总计 |
|
|
|
(1)能否据此判断有![]() 的把握认为视觉和空间能力与性别有关?
的把握认为视觉和空间能力与性别有关?
(2)经过多次测试后,甲每次解答一道几何题所用的时间在![]() 分钟,乙每次解答一道几何题所用的时间在
分钟,乙每次解答一道几何题所用的时间在![]() 分钟,现甲、乙各解同一道几何题,求乙比甲先解答完的概率.
分钟,现甲、乙各解同一道几何题,求乙比甲先解答完的概率.
(3)现从选择做几何的![]() 名女生中任意抽取两人对她们的答题情况进行全程研究,记甲、乙两女生被抽到的人数为
名女生中任意抽取两人对她们的答题情况进行全程研究,记甲、乙两女生被抽到的人数为![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]()
![]()