Question

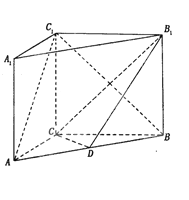
【题目】如图所示, 在直三棱柱ABC－A1B1C1中，AC＝3，BC＝4，AB=5，AA1＝4，点D是AB的中点，

（1）求证： AC1//平面CDB1；

（2）求二面角C1-AB-C的平面角的正切值.

Answer 1

【答案】（1）见解析；（3）

【解析】

（1）连接DE，得DE∥AC1，由直线与平面平行的判定定理得AC1∥平面CDB1.

（2）过点C作AB的垂线CF交AB于点F，连C1F，得∠CFC1为C﹣AB﹣C1的平面角，得FC，在Rt△C1CF中得FC，解三角形即可求二面角C﹣AB﹣C1的正切值．

（1）连接DE，由题意可知：DE为△ABC1的中位线，可知DE∥AC1，由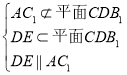 AC1∥平面CDB.

（2）过点C作AB的垂线CF交AB于点F，连C1F，∵ABC﹣A1B1C1是直三棱柱，

∴CC1⊥AB，又由AB⊥CF且CC1∩CF＝C，∴AB⊥平面CFC1，∴AB⊥FC1

于是有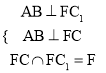 ∠CFC1为C﹣AB﹣C1的平面角，在Rt△C1CF中得FC＝＝.

在Rt△C1CF中，CC1＝4，CF ．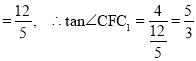

∴二面角C﹣AB﹣C1的正切值为.