题目内容
在三棱锥P-ABC中,任取两条棱,则这两条棱异面的概率是 .
分析:用列举法列出从6条棱中任取两条的方法种数,查出两条棱异面的事件数,然后利用古典概型概率计算公式求解.
解答:解:如图,
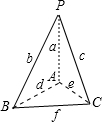
从6条棱中任取两条,利用列举法可知有15种取法,
是(a,b),(a,c),(a,d),(a,e),(a,f),(b,c),
(b,d),(b,e),(b,f),(c,d),(c,e),(c,f),
(d,e),(d,f),(e,f).
三棱锥中两条相对的棱所在是直线是异面直线,共有3对,
是(a,f),(b,e),(c,d).
∴取到两条棱异面的概率是
=
.
故答案为:
.

从6条棱中任取两条,利用列举法可知有15种取法,
是(a,b),(a,c),(a,d),(a,e),(a,f),(b,c),
(b,d),(b,e),(b,f),(c,d),(c,e),(c,f),
(d,e),(d,f),(e,f).
三棱锥中两条相对的棱所在是直线是异面直线,共有3对,
是(a,f),(b,e),(c,d).
∴取到两条棱异面的概率是
| 3 |
| 15 |
| 1 |
| 5 |
故答案为:
| 1 |
| 5 |
点评:本题考查了古典概型及其概率计算公式,考查了用列举法求时间的概率,是基础的计算题.

练习册系列答案
相关题目
 如图,在三棱锥P-ABC中,
如图,在三棱锥P-ABC中, 在三棱锥P-ABC中,AB=3,BC=4,AC=5,PA=1 面PAB⊥面CAB,面PAC⊥面CAB,则三棱锥P-ABC的体积是( )
在三棱锥P-ABC中,AB=3,BC=4,AC=5,PA=1 面PAB⊥面CAB,面PAC⊥面CAB,则三棱锥P-ABC的体积是( ) 在三棱锥P-ABC中,PA⊥平面ABC.
在三棱锥P-ABC中,PA⊥平面ABC. (2013•蚌埠二模)如图,在三棱锥P-ABC中,PA=PB=AB=2,BC=3,∠ABC=90°,平面PAB⊥平面ABC,D,E分别为AB,AC中点.
(2013•蚌埠二模)如图,在三棱锥P-ABC中,PA=PB=AB=2,BC=3,∠ABC=90°,平面PAB⊥平面ABC,D,E分别为AB,AC中点.