题目内容

5．已知正方形ABCD-A1B1C1D1的棱长为a，求异面直线AC1与A1B1所成的角的余弦值．

分析 由A1B1∥D1C1，得∠AC1D1是异面直线AC1与A1B1所成的角，由此能求出异面直线AC1与A1B1所成的角的余弦值．

解答 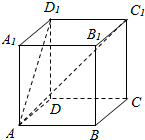解：∵A1B1∥D1C1，
∴∠AC1D1是异面直线AC1与A1B1所成的角，
∵正方形ABCD-A1B1C1D1的棱长为a，
∴AD1⊥D1C1，AC1=$\sqrt{3}a$，AD1=$\sqrt{2}a$，
∴cos∠AC1D1=$\frac{{D}_{1}{C}_{1}}{A{C}_{1}}$=$\frac{a}{\sqrt{3}a}$=$\frac{\sqrt{3}}{3}$．
∴异面直线AC1与A1B1所成的角的余弦值为$\frac{\sqrt{3}}{3}$．

点评 本题考查异面直线所成角的余弦值的求法，是基础题，解题时要认真审题，注意空间思维能力的培养．

练习册系列答案
相关题目
15．定义运算：$\overrightarrow{a}$?$\overrightarrow{b}$=|$\overrightarrow{a}$||$\overrightarrow{b}$|sinθ，其中θ为向量$\overrightarrow{a}$，$\overrightarrow{b}$的夹角，若向量$\overrightarrow{m}$，$\overrightarrow{n}$满足|$\overrightarrow{m}$|=1，|$\overrightarrow{n}$|=2，$\overrightarrow{m}•\overrightarrow{n}$=-1，则|$\overrightarrow{m}$?$\overrightarrow{n}$|的值为$\sqrt{3}$．
16．在△ABC中，已知AB=1，C=50°，当B=40°时，BC的长取最大值．
13．f（x）=ax2-c，且-4≤f（1）≤-1，-1≤f（2）≤5，则f（3）的取值范围[-1，20]．
20．设0＜a＜1，在下列四个不等式中，正确的是（　　）
A．（1-a）a＞（1+a）aB．log1-a（1+a）＜0C．（1-a）1+a＞1D．${（1-a）}^{\frac{1}{a}}$＞1
10．已知集合A={x|-1≤x≤3}，B={x|x＜2}，那么集合A∩B={x|-1≤x＜2}．
17．已知曲线上的点到点F1（0，-5），F2（0，5）的距离之差的绝对值是6，求曲线方程．
14．已知全集U=R，且集合A={x|-2＜x＜3}，集合B={x|-3≤x≤2}，求：
（1）A∪B；
（2）A∩（∁UB）．
15．中心角为135°的扇形，其面积为S1，其围成的圆锥的全面积为S2，则$\frac{{S}_{1}}{{S}_{2}}$=（　　）
A．$\frac{11}{8}$B．$\frac{13}{8}$C．$\frac{8}{11}$D．$\frac{8}{13}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网