题目内容
【题目】已知F1 , F2为椭圆E的左右焦点,点P(1, ![]() )为其上一点,且有|PF1|+|PF2|=4
)为其上一点,且有|PF1|+|PF2|=4
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)过F1的直线l1与椭圆E交于A,B两点,过F2与l1平行的直线l2与椭圆E交于C,D两点,求四边形ABCD的面积SABCD的最大值.
【答案】解:(I)设椭圆E的标准方程为 ![]() ,
,
由已知|PF1|+|PF2|=4,得2a=4,∴a=2,
又点P(1, ![]() )在椭圆上,∴
)在椭圆上,∴ ![]() ,∴b=
,∴b= ![]() ,
,
椭圆E的标准方程为 ![]() =1.
=1.
(II)由题意可知,四边形ABCD为平行四边形,
∴SABCD=4S△OAB,
设直线AB的方程为x=my﹣1,且A(x1,y1),B(x2,y2),
由 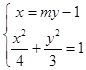 ,得(3m2+4)y2﹣6my﹣9=0,
,得(3m2+4)y2﹣6my﹣9=0,
∴y1+y2= ![]() ,y1y2=﹣
,y1y2=﹣ ![]() ,
,
S△OAB= ![]() +
+ ![]() =
= ![]() |OF1||y1﹣y2|=
|OF1||y1﹣y2|= ![]()
= ![]() =6
=6 
令m2+1=t,则t≥1,S△OAB=6 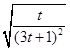 =6
=6 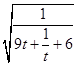
又∵g(t)=9t+ ![]() 在[1,+∞)上单调递增
在[1,+∞)上单调递增
∴g(t)≥g(1)=10,∴S△OAB的最大值为 ![]() .
.
∴SABCD的最大值为6
【解析】(I)设椭圆E的标准方程为 ![]() ,由已知|PF1|+|PF2|=4,
,由已知|PF1|+|PF2|=4, ![]() ,由此能求出椭圆E的标准方程.(II)由题意可知,四边形ABCD为平行四边形,S△ABCD=4S△OAB,设直线AB的方程为x=my﹣1,且A(x1,y1),B(x2,y2),由
,由此能求出椭圆E的标准方程.(II)由题意可知,四边形ABCD为平行四边形,S△ABCD=4S△OAB,设直线AB的方程为x=my﹣1,且A(x1,y1),B(x2,y2),由 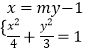 ,得(3m2+4)y2﹣6my﹣9=0,由此利用弦长公式能求出S△BCD的最大值.
,得(3m2+4)y2﹣6my﹣9=0,由此利用弦长公式能求出S△BCD的最大值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目