题目内容
8. 如图,棱长为1的正四面体在平面α上方,且棱AB?平面α,则正四面体上的所有点在平面α内的射影构成图形面积的取值范围是( )
如图,棱长为1的正四面体在平面α上方,且棱AB?平面α,则正四面体上的所有点在平面α内的射影构成图形面积的取值范围是( )| A. | [$\frac{\sqrt{2}}{4}$,$\frac{\sqrt{3}}{4}$] | B. | [$\frac{\sqrt{6}}{6}$,$\frac{\sqrt{3}}{4}$] | C. | [$\frac{\sqrt{3}}{4}$,$\frac{1}{2}$] | D. | [$\frac{\sqrt{6}}{6}$,$\frac{1}{2}$] |
分析 根据题意,当线段AB相对的侧棱CD∥α时投影面面积最大,当正四面体的侧面ABC⊥α时,投影面面积最小,求出最大、最小值即可.
解答 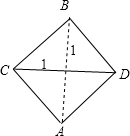 解:由题意知,当线段AB相对的侧棱与投影面平行时投影面积最大,
解:由题意知,当线段AB相对的侧棱与投影面平行时投影面积最大,
此时投影是对角线为1的正方形,如图所示;
所以投影面积为$\frac{1}{2}$×1×1=$\frac{1}{2}$;
当正四面体的侧面ABC⊥α时,投影面面积最小,
此时投影面是一个三角形,其底面边长为线段AB,长度为1,
三角形的高是点D到平面ABC的距离,为$\sqrt{{1}^{2}{-(\frac{\sqrt{3}}{2}×\frac{2}{3})}^{2}}$=$\frac{\sqrt{6}}{3}$,
如图所示;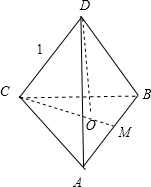
所以,该投影三角形的面积是$\frac{1}{2}$×1×$\frac{\sqrt{6}}{3}$=$\frac{\sqrt{6}}{6}$;
综上,该四面体投影面的面积取值范围是[$\frac{\sqrt{6}}{6}$,$\frac{1}{2}$].
故选:D.
点评 本题考查了三视图的应用问题,考查了空间想象能力与计算能力的应用问题,是易错题目.

练习册系列答案
相关题目
15.若直线过点M(1,2),N(4,2+$\sqrt{3}$),则此直线的倾斜角为( )
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
16.抛物线y2=2px(p>0)的焦点为F,点A,B在此抛物线上,且∠AFB=90°,弦AB的中点M在该抛物线准线上的射影为M′,则$\frac{|MM′|}{|AB|}$的最大值为( )
| A. | $\sqrt{3}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | 1 | D. | $\frac{{\sqrt{2}}}{2}$ |
13.已知函数f(x)=$\left\{\begin{array}{l}(4-a)x,x<2\\{a^x},x≥2\end{array}\right.$在R上单调递增,则a的取值范围是( )
| A. | (1,4] | B. | (2,4) | C. | [2,4) | D. | (4,+∞) |
17.在等比数列{an}前n项和Sn=5n-1,则a12+a22+a32+…+an2等于( )
| A. | (5n-1)2 | B. | 52n-1 | C. | $\frac{2}{3}$(52n+1+1) | D. | $\frac{2}{3}$(52n-1) |