题目内容
在平面四边形ABCD中, ABC为正三角形,
ABC为正三角形, ADC为等腰直角三角形,AD=DC=2,将
ADC为等腰直角三角形,AD=DC=2,将 ABC沿AC折起,使点B至点P,且PD=2
ABC沿AC折起,使点B至点P,且PD=2 ,M为PA的中点,N在线段PD上。
,M为PA的中点,N在线段PD上。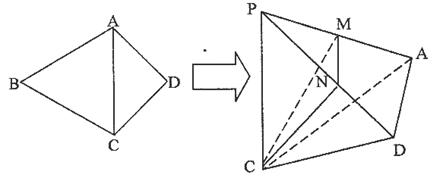
(I)若PA 平面CMN,求证:AD//平面CMN;
平面CMN,求证:AD//平面CMN;
(II)求直线PD与平面ACD所成角的余弦值。
(I) 在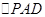 中
中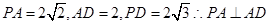 ,因为PA
,因为PA 平面CMN
平面CMN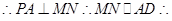 AD//平面CMN (II)
AD//平面CMN (II) 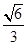
解析试题分析:(I)在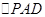 中
中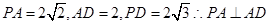 ,因为PA
,因为PA 平面CMN
平面CMN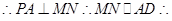 AD//平面CMN
AD//平面CMN
(II)取AC中点E,连接PE,DE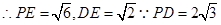
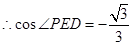
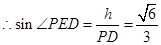

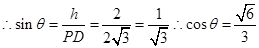
考点:线面平行的判定与线面角的求解
点评:证明线面平行通常证明直线平行于平面内一条直线,将线面平行问题转化为线线平行问题,求线面所成角需要找到斜线段长度,垂线段长度及斜线段在平面内的射影长度中的两个,解三角形即可求出

练习册系列答案
相关题目
 中,侧棱与底面垂直,
中,侧棱与底面垂直,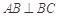 ,
,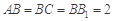 ,
,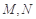 分别是
分别是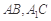 的中点
的中点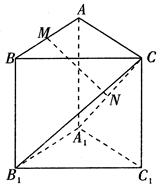
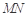 ∥平面
∥平面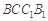 ;
;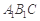 ;
;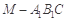 的体积.
的体积.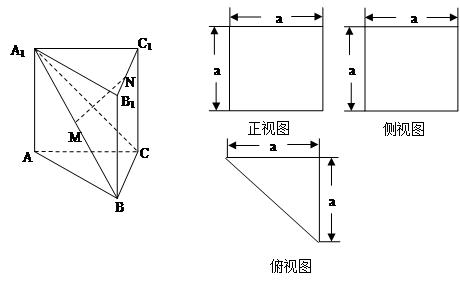
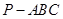 的三视图如图所示.
的三视图如图所示.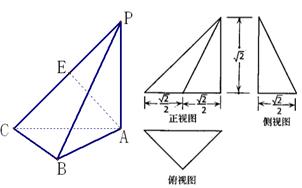
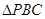 是直角三角形;
是直角三角形;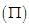 求三棱锥
求三棱锥 在线段
在线段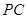 上何处时,
上何处时,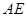 与平面
与平面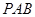 所成的角为
所成的角为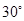 .
. ABC的边AB,BC,CA上分别取D,E,F.使得DE=BE,FE=CE,又点O是△ADF的外心。
ABC的边AB,BC,CA上分别取D,E,F.使得DE=BE,FE=CE,又点O是△ADF的外心。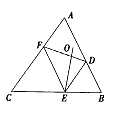
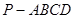 中,底面
中,底面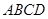 为平行四边形,
为平行四边形,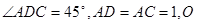 为
为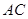 中点,
中点,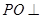 面
面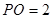 ,
, 为
为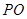 中点。
中点。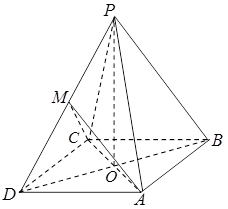
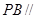 面
面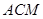 。
。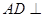 面
面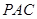 。
。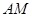 与平面
与平面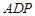 的最大面积及相应的x值.
的最大面积及相应的x值.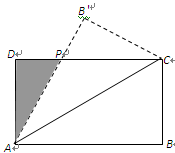
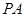 垂直于⊙
垂直于⊙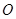 所在的平面,
所在的平面,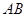 是⊙
是⊙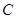 是⊙
是⊙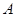 作
作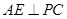 ,垂足为
,垂足为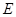 .
. 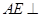 平面
平面