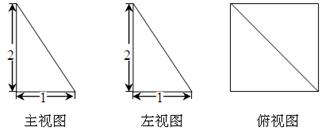
题目内容
一个多面体的直观图、正视图、侧视图、俯视图如图所示,M、N分别为A1B、B1C1的中点.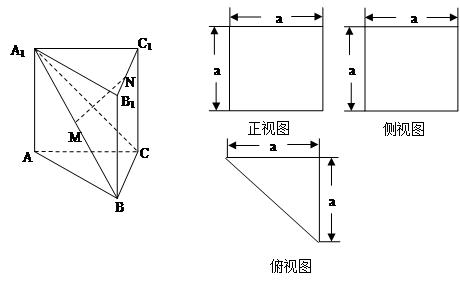
(1)求证:MN//平面ACC1A1;
(2)求证:MN^平面A1BC.
(1)见解析;(2)见解析
解析试题分析:先由三视图还原几何体的直观图中线段长度,(1)利用直线与平面平行的判定定理,在平面内找一直线AC1,由三角形中位线证明MN//AC1,用直线与平面平行的判定定理得到结论;(2)通过证明平面内两相交直线同时垂直MN,由直线与平面垂直的判定定理得证.
试题解析:证明:由意可得:这个几何体是直三棱柱,
且AC^BC,AC=BC=CC1 -----2分
(1)由直三棱柱的性质可得:AA1^A1B1
四边形ABCD为矩形,则M为AB1的中点,N为B1C1
的中点,在DAB1C中,由中位线性质可得:
MN//AC1,又AC1Ì平面ACC1A1,MNË平面ACC1A1
\ MN//平面ACC1A1 6分
(2)因为:CC1^平面ABC,BCÌ平面ABC,\ CC1^ BC,
又BC^AC,ACÇCC1=C,所以,BC^平面ACC1A1,AC1Ì平面ACC1A1
\ BC^AC1,在正方形ACC1A1中,AC1^A1C,BCÇA1C=C,\ AC1^平面A1BC,
又AC1//MN,\MN^平面A1BC 10分
考点:1.三视图;2.直线与平面的平行、垂直的判定

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
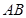 和AB1的中点,点F在BC上且满足BF∶FC=1∶3.
和AB1的中点,点F在BC上且满足BF∶FC=1∶3.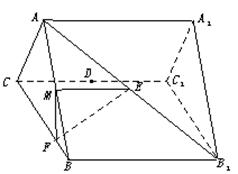
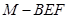 的体积.
的体积.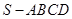 中,侧棱
中,侧棱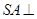 底面
底面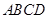 ,且底面
,且底面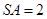 ,
,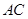 与
与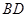 相交于点
相交于点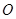 .
.
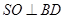 ;
;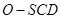 的体积.
的体积. ,BD=CD=1,另一个侧面ABC是正三角形.
,BD=CD=1,另一个侧面ABC是正三角形.
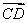 的方向相同时,画出三棱锥A—BCD的三视图;(要求标出尺寸)
的方向相同时,画出三棱锥A—BCD的三视图;(要求标出尺寸)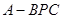 中,
中,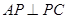 ,
,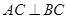 ,
,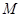 为
为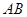 中点,
中点,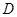 为
为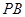 中点,且
中点,且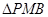 为正三角形。
为正三角形。
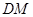 //平面
//平面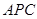 ;
;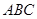 ⊥平面
⊥平面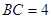 ,
,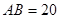 ,求三棱锥
,求三棱锥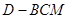 的体积.
的体积.
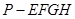 ,下半部分是长方体
,下半部分是长方体 。图2、图3分别是该标识墩的正(主)视图和俯视图。
。图2、图3分别是该标识墩的正(主)视图和俯视图。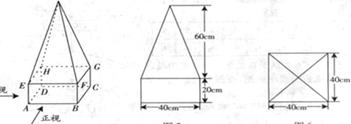
 ABC为正三角形,
ABC为正三角形, ,M为PA的中点,N在线段PD上。
,M为PA的中点,N在线段PD上。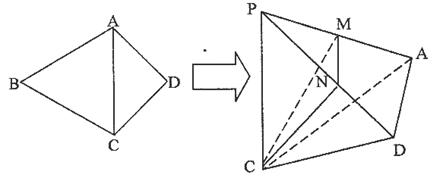
 平面CMN,求证:AD//平面CMN;
平面CMN,求证:AD//平面CMN;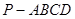 ,
,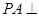 底面ABCD,其三视图如下,若M是PD的中点
底面ABCD,其三视图如下,若M是PD的中点