题目内容
在直角坐标平面中,已知点![]() ,
, ![]() ,…
,…![]() , 其中n是正整数. 对平面上任一点
, 其中n是正整数. 对平面上任一点![]() , 记A1为A0关于点P1的对称点, A2为A1关于点P2的对称点, ┄, AN为AN-1关于点PN的对称点.
, 记A1为A0关于点P1的对称点, A2为A1关于点P2的对称点, ┄, AN为AN-1关于点PN的对称点.
(1)求向量![]() 的坐标;
的坐标;
(2)当点A0在曲线C上移动时, 点A2的轨迹是函数![]() 的图象,其中
的图象,其中![]() 是以3为周期的周期函数,且当x∈(0,3)时,
是以3为周期的周期函数,且当x∈(0,3)时,![]() =lgx.求以曲线C为图象的函数在(1,4)上的解析式;
=lgx.求以曲线C为图象的函数在(1,4)上的解析式;
(3)对任意偶数n,用n表示向量![]() 的坐标.
的坐标.
解:(1)法一: 设点A0(x,y), A1为A0关于点P1的对称点,A1的坐标为(2-x,4-y),
A2为A1关于点P2的对称点,A2的坐标为(2+x,4+y),
∴![]() =(2,4).
=(2,4).
法二:![]() =2
=2![]() , ∴
, ∴![]() =(2,4)
=(2,4)
(2) 法一∵![]() =(2,4),
=(2,4),
∴f(x)的图象由曲线C向右平移2个单位,再向上平移4个单位得到.因此,
曲线C是函数y=g(x)的图象,其中g(x)是以3为周期的周期函数,
且当x∈(-2,1]时,g(x)=lg(x+2)-4.于是, 当x∈(1,4)时, g(x)=lg(x-1)-4.
法二:设点A0(x,y), 则A2的坐标为(2+x,4+y)
∵点A2的轨迹是函数y=f(x)的图象,于是当0<x+2≤3时,有y+4=lg(x+2),
即当-2< x≤1时, g(x)=y=lg(x+2)-4.
∴当x∈(1,4)时,g(x)=lg(x-1)-4.
(3)![]() =
=![]() , 由于
, 由于![]() ,得
,得
![]() =2(
=2(![]() ) =2((1,2)+(1,23)+…+(1,2n-1))
) =2((1,2)+(1,23)+…+(1,2n-1))
=2(![]() ,
,![]() ) = (n,
) = (n,![]() )
)

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 的坐标;
的坐标; ,
, ,对平面上任意一点
,对平面上任意一点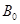 ,记
,记 为
为 的对称点,
的对称点, 为
为 的对称点,
的对称点, 为
为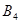 为
为 为
为 关于
关于 为
为 为
为 …。则
…。则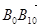 =
=