题目内容
学校游园活动有这样一个游戏项目:甲箱子里装有3个白球、2个黑球,乙箱子里装有1个白球、2个黑球,这些球除颜色外完全相同,每次游戏从这两个箱子里各随机摸出2个球,若摸出的白球不少于2个,则获奖.(每次游戏结束后将球放回原箱)
(Ⅰ)求在1次游戏中,
(i)摸出3个白球的概率;
(ii)获奖的概率;
(Ⅱ)求在2次游戏中获奖次数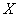 的分布列及数学期望
的分布列及数学期望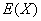
(Ⅰ)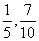 (Ⅱ)
(Ⅱ)
解析试题分析:(I)(i)解:设“在1次游戏中摸出i个白球”为事件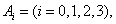 则
则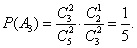
(ii)解:设“在1次游戏中获奖”为事件B,则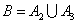 ,又
,又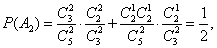
且A2,A3互斥,所以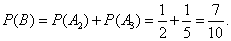
(II)解:由题意可知X的所有可能取值为0,1,2.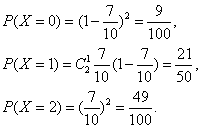
所以X的分布列是
X的数学期望 X 0 1 2 P 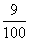
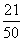
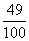
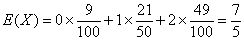
另解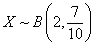 ,
, 
考点:独立重复试验
点评:本题游戏结束后将球放回原箱,则这种游戏是独立重复试验。对于独立重复试验,其概率的求法是: (一般地,如果在一次试验中某事件发生的概率是P,那么在n次独立重复试验中这个事件恰好发生k次的概率)。
(一般地,如果在一次试验中某事件发生的概率是P,那么在n次独立重复试验中这个事件恰好发生k次的概率)。

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
甲,乙两人进行射击比赛,每人射击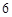 次,他们命中的环数如下表:
次,他们命中的环数如下表:
| 甲 | 5 | 8 | 7 | 9 | 10 | 6 |
| 乙 | 6 | 7 | 4 | 10 | 9 | 9 |
(Ⅱ)把甲6次射击命中的环数看成一个总体,用简单随机抽样方法从中抽取两次命中的环数组成一个样本,求该样本平均数与总体平均数之差的绝对值不超过
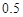 的概率.
的概率. 某品牌汽车4S店对最近100位采用分期付款的购车者进行统计,统计结果如下表所示:
| 付款方式 | 分1期 | 分2期 | 分3期 | 分4期 | 分5期 |
| 频数 | 40 | 20 |  | 10 |  |
(Ⅰ)求上表中
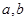 的值;
的值;(Ⅱ)若以频率作为概率,求事件
 :“购买该品牌汽车的3位顾客中,至多有一位采用3期付款”的概率
:“购买该品牌汽车的3位顾客中,至多有一位采用3期付款”的概率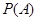 ;
;(Ⅲ)求Y的分布列及数学期望EY.
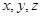 分别表示甲,乙,丙3个盒中的球数.
分别表示甲,乙,丙3个盒中的球数.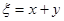 ,求随机变量
,求随机变量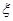 的概率分布列和数学期望.
的概率分布列和数学期望.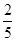 ;从袋中任意摸出2个球,至少得到1个白球的概率是
;从袋中任意摸出2个球,至少得到1个白球的概率是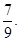
 ,从B中摸出一个红球的概率为p.
,从B中摸出一个红球的概率为p. ,求随机变量
,求随机变量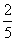 ,求p的值。
,求p的值。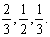 用
用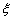 表示被招聘的人数。
表示被招聘的人数。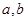 .
.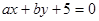 与圆
与圆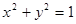 相切的概率;
相切的概率;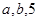 的值分别作为三条线段的长,求这三条线段能围成等腰三角形的概率.
的值分别作为三条线段的长,求这三条线段能围成等腰三角形的概率.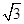 ,在BC边上任取一点M,求
,在BC边上任取一点M,求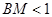 的概率.
的概率.