题目内容
在进行一项掷骰子放球游戏中,规定:若掷出1点,甲盒中放一球;
若掷出2点或3点,乙盒中放一球;若掷出4点或5点或6点,丙盒中放一球,前后共掷3
次,设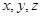 分别表示甲,乙,丙3个盒中的球数.
分别表示甲,乙,丙3个盒中的球数.
(1)求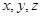 依次成公差大于0的等差数列的概率;
依次成公差大于0的等差数列的概率;
(2)记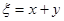 ,求随机变量
,求随机变量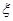 的概率分布列和数学期望.
的概率分布列和数学期望.
(1)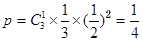 (2)随机变量
(2)随机变量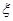 的概率分布列
的概率分布列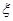
0 1 2 3 P 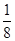
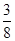
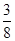
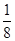
数学期望为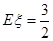
解析试题分析:解:(1)x,y,z依次称公差大于0的等差数列的概率,即甲,乙,丙3个盒中的球数。
分别为0,1,2,此时的概率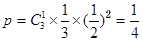
(2)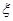 的取值范围0,1,2,3,且
的取值范围0,1,2,3,且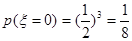 ;
;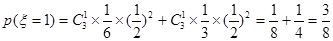 ;
;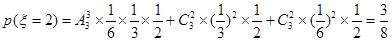 ;
;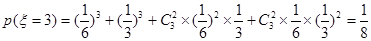 .
.
随机变量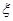 的概率分布列
的概率分布列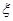
0 1 2 3 P 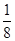
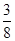
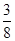
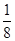
数学期望为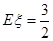
考点:随机变量的分布列;数学期望
点评:求随机变量的分布列和数学期望是常考题型,解决这种题目关键是求出随机变量对应的概率。

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
某批发市场对某种商品的日销售量(单位:吨)进行统计,最近50天的统计结果如下表:
| 日销售量(吨) | 1 | 1.5 | 2 |
| 天数 | 10 | 25 | 15 |
(2)若以频率为概率,且每天的销售量相互独立.
①求5天中该种商品恰有2天的销售量为1.5吨的概率;
②已知每吨该商品的销售利润为2万元,X表示该种商品两天销售利润的和,求X的分布列和数学期望.
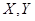 分别表示这4个人中去参加甲、乙项目联欢的人数,记
分别表示这4个人中去参加甲、乙项目联欢的人数,记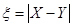 ,求随机变量
,求随机变量 的分布列与数学期望
的分布列与数学期望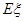 .
.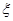 ,求
,求 )获得身高数据的茎叶图如下:
)获得身高数据的茎叶图如下: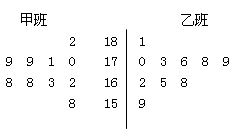
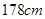 的同学,求至少有一名身高大于
的同学,求至少有一名身高大于 的同学被抽中的概率。
的同学被抽中的概率。
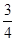 ,设第三组中被抽中的学生有
,设第三组中被抽中的学生有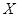 名获得优秀,求
名获得优秀,求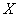 的分布列及数学期望
的分布列及数学期望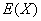
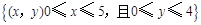 内任取一个元素,能使代数式
内任取一个元素,能使代数式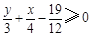 的概率是多少?
的概率是多少?