题目内容
)袋中装有大小相同的黑球、白球和红球共10个。已知从袋中任意摸出1个球,得到黑球的概率是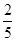 ;从袋中任意摸出2个球,至少得到1个白球的概率是
;从袋中任意摸出2个球,至少得到1个白球的概率是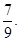
(1)求袋中各色球的个数;
(2)从袋中任意摸出3个球,记得到白球的个数为ξ,求随机变量ξ的分布列及数学期望Eξ和方差Dξ;
(1)袋中白球5个,黑球4个,红球1个(2)ξ 0 1 2 3 P 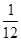
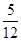
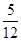
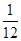
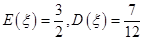
解析试题分析:(1)因为从袋中任意摸出1球得到黑球的概率是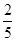 ,故设黑球个数为x,则
,故设黑球个数为x,则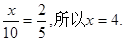
设白球的个数为y,又从袋中任意摸出2个球,至少得到1个白球的概率是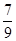 ,则
,则
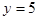 ,故袋中白球5个,黑球4个,红球1个。 6分
,故袋中白球5个,黑球4个,红球1个。 6分
(2)由题设知ξ的所有取值是0,1,2,3,则随机变量ξ的分布列为ξ 0 1 2 3 P 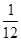
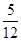
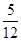
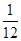
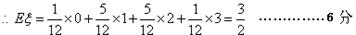
 12分
12分
考点:古典概型概率与分布列
点评:第一问古典概型概率的考查,需找到所有基本事件种数与满足题意要求的基本事件种数求其比值,第二问求分布列的题目首先找到随机变量取的值,然后求出其概率,汇总成分布列,由分布列可求出期望方差

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
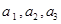 ,女生2名,记为
,女生2名,记为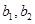 ,现从中任选2名学生去参加校数学竞赛
,现从中任选2名学生去参加校数学竞赛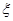 ,求
,求
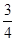 ,设第三组中被抽中的学生有
,设第三组中被抽中的学生有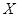 名获得优秀,求
名获得优秀,求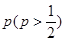 ,且各局胜负相互独立.已知
,且各局胜负相互独立.已知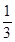 .
.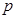 的值;
的值; 表示比赛停止时已比赛的局数,求随机变量
表示比赛停止时已比赛的局数,求随机变量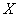 的分布列及数学期望
的分布列及数学期望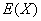
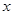 个红球,
个红球,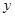 个白球(
个白球( ,且
,且 );乙的箱子里面放有2个红球,1个白球,1个黄球.现在甲从自己的箱子里任取2个球,乙从自己的箱子里任取1个球.若取出的3个球颜色都不相同,则甲获胜.
);乙的箱子里面放有2个红球,1个白球,1个黄球.现在甲从自己的箱子里任取2个球,乙从自己的箱子里任取1个球.若取出的3个球颜色都不相同,则甲获胜. 的分布列.
的分布列.