题目内容
已知函数f(x)＝－x2－2x，g(x)＝
(1)g[f(1)]＝________；
(2)若方程g[f(x)]－a＝0的实数根的个数有4个，则a的取值范围是________．
(1)g[f(1)]＝________；
(2)若方程g[f(x)]－a＝0的实数根的个数有4个，则a的取值范围是________．
(1)－2，(2)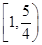 
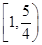
(1)利用解析式直接求解得g[f(1)]＝g(－3)＝－3＋1＝－2；
(2)令f(x)＝t，则g(t)＝a，要使原方程有4解，则方程f(x)＝t在t＜1时有2个不同解，即函数y＝g(t)，t＜1与y＝a有两个不同的交点，作出函数y＝g(t)，t＜1的图象，由图象可知1≤a＜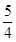
时，函数y＝g(t)，t＜1与y＝a有两个不同的交点，即所求a的取值范围是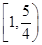
(2)令f(x)＝t，则g(t)＝a，要使原方程有4解，则方程f(x)＝t在t＜1时有2个不同解，即函数y＝g(t)，t＜1与y＝a有两个不同的交点，作出函数y＝g(t)，t＜1的图象，由图象可知1≤a＜
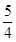时，函数y＝g(t)，t＜1与y＝a有两个不同的交点，即所求a的取值范围是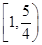
练习册系列答案
星级口算天天练系列答案
芒果教辅达标测试卷系列答案
相关题目
，
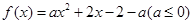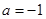，求函数的零点；
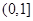上恰有一个零点，求
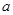的取值范围．
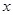的方程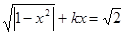
有3个不等实数根，则实数
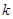的取值范围为____________.
则函数h(x)＝f(x)－g(x)在区间[－5,4]内的零点的个数( )．
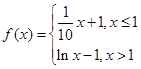，则方程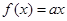
恰有两个不同实数根时，实数
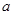的取值范围是（ ）（注：
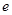为自然对数的底数）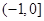
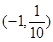
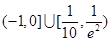
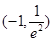
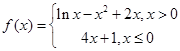的零点个数是 ．