题目内容
11.函数f(x)=x+2cosx在区间[0,π]上的最大值为( )| A. | 2 | B. | π-2 | C. | $\sqrt{3}+\frac{5π}{6}$ | D. | $\sqrt{3}+\frac{π}{6}$ |
分析 先求出函数f(x)的导数,得到函数的单调区间,从而求出函数的最大值.
解答 解:f′(x)=1-2sinx,
令f′(x)>0,解得:x<$\frac{π}{6}$或x>$\frac{5π}{6}$,
令f′(x)<0,解得:$\frac{π}{6}$<x<$\frac{5π}{6}$,
∴函数f(x)在[0,$\frac{π}{6}$),($\frac{5π}{6}$,π]递增,在($\frac{π}{6}$,$\frac{5π}{6}$)递减,
∴f(x)极大值=f($\frac{π}{6}$)=$\sqrt{3}$+$\frac{π}{6}$,f(x)极小值=f($\frac{5π}{6}$)=$\frac{5π}{6}$-$\sqrt{3}$,
又f(0)=2,f(π)=π-2,
故所求最大值为$\sqrt{3}$+$\frac{π}{6}$.
点评 本题考查了函数的单调性、函数的最值问题,考查导数的应用,是一道基础题.

练习册系列答案
相关题目
1.若(3$\sqrt{x}$-$\frac{1}{\sqrt{x}}$)n 的展开式中各项系数之和为256,则展开式的常数项是( )
| A. | 第3项 | B. | 第4项 | C. | 第5项 | D. | 第6项 |
19.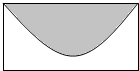 如图的矩形,长为5,宽为2,在矩形内随机地撒300颗黄豆,数得落在阴影部分的黄豆数为138颗,则可以估计出阴影部分的面积约为( )
如图的矩形,长为5,宽为2,在矩形内随机地撒300颗黄豆,数得落在阴影部分的黄豆数为138颗,则可以估计出阴影部分的面积约为( )
 如图的矩形,长为5,宽为2,在矩形内随机地撒300颗黄豆,数得落在阴影部分的黄豆数为138颗,则可以估计出阴影部分的面积约为( )
如图的矩形,长为5,宽为2,在矩形内随机地撒300颗黄豆,数得落在阴影部分的黄豆数为138颗,则可以估计出阴影部分的面积约为( )| A. | $\frac{23}{11}$ | B. | $\frac{23}{10}$ | C. | $\frac{23}{6}$ | D. | $\frac{23}{5}$ |
6.使|x-4|+|x-5|<a有实数解的a为( )
| A. | a>1 | B. | 1<a<9 | C. | a>1 | D. | a≥1 |
3.下列函数中既是偶函数,又在区间(0,+∞)上单调递增的函数式( )
| A. | y=x3 | B. | y=-x3+1 | C. | y=|x|+1 | D. | y=2x |
4.在△ABC中,b2cosC+bccosB=a2,则△ABC的形状是( )
| A. | 直角三角形 | B. | 锐角三角形 | C. | 等腰直角三角形 | D. | 等腰三角形 |