题目内容
【题目】已知函数f(x)![]() ,g(x)
,g(x)![]() 1.
1.
(1)若f(a)=2,求实数a的值;
(2)判断f(x)的单调性,并证明;
(3)设函数h(x)=g(x)![]() (x>0),若h(2t)+mh(t)+4>0对任意的正实数t恒成立,求实数m的取值范围.
(x>0),若h(2t)+mh(t)+4>0对任意的正实数t恒成立,求实数m的取值范围.
【答案】(1)a=log23;(2)函数f(x)在(﹣∞,0),(0,+∞)上单调递减,证明见解析(3)[﹣3,+∞).
【解析】
(1)根据f(a)=2,代入解析式求解.
(2)函数f(x)在(﹣∞,0),(0,+∞)上单调递减,用单调性的定义证明.
(3)化简得到![]() ,将
,将![]() 0对任意的正实数t恒成立,通过换元
0对任意的正实数t恒成立,通过换元![]() ,μ∈(2,+∞),转化为μ2+mμ+2>0对任意μ∈(2,+∞)恒成立,即
,μ∈(2,+∞),转化为μ2+mμ+2>0对任意μ∈(2,+∞)恒成立,即![]() 对任意μ∈(2,+∞)恒成立,再求解
对任意μ∈(2,+∞)恒成立,再求解![]() 最大值即可.
最大值即可.
(1)∵![]() ,
,
∴2a=3,
∴a=log23;
(2)函数f(x)在(﹣∞,0),(0,+∞)上单调递减,
证明如下:
函数的定义域为(﹣∞,0)∪(0,+∞),
因为f(-x)![]()
所以f(x)是奇函数
任取![]() 且
且![]()
![]() ,
,
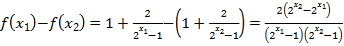
因为![]()
所以![]()
因为![]()
所以![]()
所以![]()
所以f(x)在(0,+∞)上单调递减,
又因为f(x)是奇函数
故函数f(x)在(﹣∞,0),(0,+∞)上单调递减;
(3)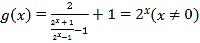 ,
,![]() ,
,
∴![]() 0对任意的正实数t恒成立,
0对任意的正实数t恒成立,
令![]() ,则μ∈(2,+∞),
,则μ∈(2,+∞),
∴μ2+mμ+2>0对任意μ∈(2,+∞)恒成立,
即![]() 对任意μ∈(2,+∞)恒成立,
对任意μ∈(2,+∞)恒成立,
又![]() 在(2,+∞)上单调递减,故
在(2,+∞)上单调递减,故![]() ,
,
则m≥﹣3,即实数m的取值范围为[﹣3,+∞).

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目