题目内容
【题目】在四面体![]() 中,
中, ![]() 底面
底面![]() 为
为![]() 的重心,
的重心, ![]() 为线段
为线段![]() 上一点,且
上一点,且![]() 平面
平面![]() ,则直线
,则直线![]() 与
与![]() 所成角的余弦值为__________.
所成角的余弦值为__________.
【答案】![]()
【解析】在三棱锥D-ABC中,取AB的中点E,连接CE,在CE上取点G使得CG=2GE,则![]() 为
为![]() 的重心,取EB的三等分点M,即MB=2EM,则有MG平行于BC,MB=2,又
的重心,取EB的三等分点M,即MB=2EM,则有MG平行于BC,MB=2,又![]() ,所以AM=2MB,同样在线段AD上取点F,使得FM平行于DB,即有AF=2FD,连接FG,因为
,所以AM=2MB,同样在线段AD上取点F,使得FM平行于DB,即有AF=2FD,连接FG,因为![]() 得到面FGN
得到面FGN![]() 面DBC,则FG
面DBC,则FG![]() 面DBC
面DBC
取AE的三等分点N,使得AN=2NE,则NG平行于AC,连接FN,则![]() 即为直线
即为直线![]() 与
与![]() 所成角,NG=
所成角,NG=![]() AC=
AC=![]() ,
, ![]() ,
, ![]() ,
,
延长AG交BC于点Q,则AG=![]() AQ,又
AQ,又![]() ,利用
,利用![]() (
(![]() )平方得 AQ=
)平方得 AQ=![]() ,则AG=
,则AG=![]() ,FA=4所以FG=
,FA=4所以FG=![]() ,在
,在![]() FGN中,
FGN中, 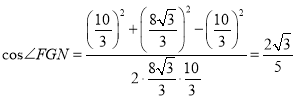
故答案为![]()

练习册系列答案
相关题目
【题目】某校在高三抽取了500名学生,记录了他们选修A、B、C三门课的选修情况,如表:
科目 学生人数 | A | B | C |
120 | 是 | 否 | 是 |
60 | 否 | 否 | 是 |
70 | 是 | 是 | 否 |
50 | 是 | 是 | 是 |
150 | 否 | 是 | 是 |
50 | 是 | 否 | 否 |
(Ⅰ)试估计该校高三学生在A、B、C三门选修课中同时选修2门课的概率.
(Ⅱ)若该高三某学生已选修A,则该学生同时选修B、C中哪门的可能性大?