题目内容
【题目】已知函数![]() ,且
,且![]() .
.
![]() 求定义域;
求定义域;
![]() 若函数
若函数![]() 的反函数是其本身,求a的值;
的反函数是其本身,求a的值;
![]() 求函数
求函数![]() 的值域.
的值域.
【答案】(1)![]() ; (2)
; (2)![]() ;(3) 当
;(3) 当![]() 时,函数的值域是
时,函数的值域是![]() ;当
;当![]() 时,函数的值域是
时,函数的值域是![]() .
.
【解析】
(1)由函数解析式的特征得到关于![]() 的不等式,解不等式可得所求结果;(2)求出函数的反函数,利用条件中给出的相等关系式求出
的不等式,解不等式可得所求结果;(2)求出函数的反函数,利用条件中给出的相等关系式求出![]() 的值;(3)先求出函数
的值;(3)先求出函数![]() 的定义域,然后通过分类讨论得到函数的值域即可.
的定义域,然后通过分类讨论得到函数的值域即可.
(1)由![]() ,得
,得![]() ,
,
解得![]() ;
;
所以函数的定义域为![]() .
.
(2)由![]() ,且
,且![]() ,解得
,解得![]() ,
,
互换![]() ,得
,得![]() ,
,
所以函数的反函数为![]() .
.
由于函数![]() 的反函数是其本身,
的反函数是其本身,
所以![]() .
.
(3)由题意得![]()
![]() ,
,
由![]() ,得
,得![]() ,
,
∴函数![]() 的定义域为
的定义域为![]() .
.
∵![]() ,当且仅当
,当且仅当![]() 时等号成立,
时等号成立,
∴![]() ,
,
故![]() 的取值范围是
的取值范围是![]() .
.
①当![]() 时,
时,![]() ,
,
∴函数![]() 的值域是
的值域是![]() .
.
②当![]() 时,
时,![]() ,
,
∴函数![]() 的值域是
的值域是![]() .
.
综上可得,当![]() 时,函数的值域是
时,函数的值域是![]() ;当
;当![]() 时,函数的值域是
时,函数的值域是![]() .
.

练习册系列答案
相关题目
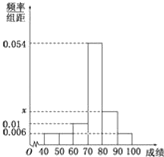
【题目】2019年![]() 月湖北潜江将举办第六届“中国湖北(潜江)龙虾节”,为了解不同年龄的人对“中国湖北(潜江)龙虾节”关注程度,某机构随机抽取了年龄在
月湖北潜江将举办第六届“中国湖北(潜江)龙虾节”,为了解不同年龄的人对“中国湖北(潜江)龙虾节”关注程度,某机构随机抽取了年龄在![]() 岁之间的
岁之间的![]() 人进行调查,经统计“年轻人”与“中老年人”的人数之比为
人进行调查,经统计“年轻人”与“中老年人”的人数之比为![]() .
.
关注 | 不关注 | 合计 | |
年轻人 |
| ||
中老年人 | |||
合计 |
|
|
|
(1)根据已知条件完成上面的![]() 列联表,并判断能否有
列联表,并判断能否有![]() 的把握认为关注“中国湖北(潜江)龙虾节”是否和年龄段有关?
的把握认为关注“中国湖北(潜江)龙虾节”是否和年龄段有关?
(2)现已用分层抽样的办法从中老年人中选取了![]() 人进行问卷调查.若再从这
人进行问卷调查.若再从这![]() 人中选取
人中选取![]() 人进行面对面询问,求事件“选取的
人进行面对面询问,求事件“选取的![]() 人中恰有
人中恰有![]() 人关注“中国湖北(潜江)龙虾节””的概率.
人关注“中国湖北(潜江)龙虾节””的概率.
附:参考公式![]() ,其中
,其中![]() .
.
临界值表:
|
|
|
|
|
|
|
|