题目内容
【题目】设△ABC是边长为1的正三角形，点P1 ， P2 ， P3四等分线段BC（如图所示）．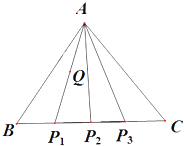
（1）求 
+ 
的值；
（2）Q为线段AP1上一点，若 
=m + 
，求实数m的值．
【答案】
（1）解： 
+ 
= （ + ）=（ + 
）（ + + 
）=（ + 
）（2 + 
）=2 
+ + 
2=2﹣1×1× + = 
，
（2）解：设 
=λ ，
∴ =λ =λ（ + ）=λ + 
（ 
﹣ ）= 
λ + =m + 
，
∴ = ， 
=m，
解得m= ．
【解析】分别向量的几何意义和向量的数量积的运算计算即可．
【考点精析】解答此题的关键在于理解平面向量的基本定理及其意义的相关知识，掌握如果
、
是同一平面内的两个不共线向量，那么对于这一平面内的任意向量
，有且只有一对实数
、
，使
．
练习册系列答案
相关题目
【题目】某地农业监测部门统计发现：该地区近几年的生猪收购价格每四个月会重复出现，但生猪养殖成本逐月递增．下表是今年前四个月的统计情况：
月份 | 1月份 | 2月份 | 3月份 | 4月份 |
收购价格（元/斤） | 6 | 7 | 6 | 5 |
养殖成本（元/斤） | 3 | 4 | 4.6 | 5 |
现打算从以下两个函数模型：
①y=Asin（ωx+φ）+B，（A＞0，ω＞0，﹣π＜φ＜π），
②y=log2（x+a）+b
中选择适当的函数模型，分别来拟合今年生猪收购价格（元/斤）与相应月份之间的函数关系、养殖成本（元/斤）与相应月份之间的函数关系．
（1）请你选择适当的函数模型，分别求出这两个函数解析式；
（2）按照你选定的函数模型，帮助该部门分析一下，今年该地区生猪养殖户在8月和9月有没有可能亏损？
