题目内容
在直角坐标系中，已知△AOB三边所在直线的方程分别为x=0，y=0，2x+3y=30，则△AOB内部和边上整点（即横、纵坐标均为整数的点）的总数是
91
91
．分析：我们要先画出△AOB即直线x=0，y=0，2x+3y=30，围成的平面区域，然后分析平面区域里各个点，讨论y的取值，进一步求出满足条件的x的个数，从而求出所求．
解答：解：△AOB即直线x=0，y=0，2x+3y=30围成的平面区域
如图所示：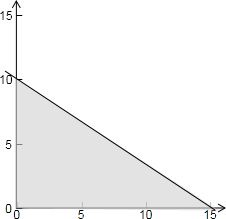
当y=0，有16个整点；当y=1，有14个整点；
当y=2，有13个整点；当y=3，有11个整点；
当y=4，有10个整点；当y=5，有8个整点；
当y=6，有7个整点；当y=7，有5个整点；
当y=8，有4个整点；当y=9，有2个整点；
当y=10，有1个整点；
共91个整点．
故答案为：91．
如图所示：
当y=0，有16个整点；当y=1，有14个整点；
当y=2，有13个整点；当y=3，有11个整点；
当y=4，有10个整点；当y=5，有8个整点；
当y=6，有7个整点；当y=7，有5个整点；
当y=8，有4个整点；当y=9，有2个整点；
当y=10，有1个整点；
共91个整点．
故答案为：91．
点评：本题主要考查求平面区域的整点个数，是线性规划问题中一类重要题型，在解题时，关键是正确地画出平面区域，然后分析平面区域内的点，易求出平面区域内的整点个数，属于基础题．
练习册系列答案
相关题目
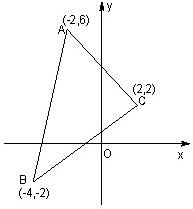如图，在直角坐标系中，已知△ABC的三个顶点的坐标，求：
如图，在直角坐标系中，已知射线OA：x-y=0（x≥0），OB：