题目内容
【题目】已知动圆
与圆
内切，与圆
外切，记圆心的轨迹为曲线
.
（1）求曲线的方程.
（2）直线
与曲线交于点
，
，点
为线段
的中点，若
，求
面积的最大值.
【答案】（1）
（2）
【解析】
（1）推导出|PE|+|PF|＝4＞|EF|＝2
，从而圆心P的轨迹C为以E与F为焦点的椭圆，由此能求出曲线C的方程．
（2）设直线l：x＝my+n，由方程组
，得（4+m2）y2+2mny+n2﹣4＝0，由此利用韦达定理、弦长公式，结合已知条件能求出直线l的方程．
（1）设动圆
的半径为
，由已知得
，
，则有
，
∴的轨迹是以
，
为焦点的椭圆，设曲线
的方程为
，易知
，
，则
，
∴曲线的方程为.
（2）设直线
，
，
，
由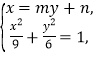
得
①
，
，
，
由中点坐标公式可知
.
，
②，
设直线
与
轴的交点为
，则点的坐标为
，
则
面积的平方
，
设
，
则
，当
，即
时，的面积取得最大值.
练习册系列答案
小题狂做系列答案
相关题目
