题目内容
16.已知a,b,c均为正数,求证:a3+b3+c3≥a2b+b2c+c2a.分析 不妨设a≥b≥c>0,则a2≥b2≥c2,由排序原理:反序和≤乱序和≤同序和,即可得证.
解答 证明:不妨设a≥b≥c>0,
∴a2≥b2≥c2,
由排序原理:反序和≤乱序和≤同序和,得
a•a2+b•b2+c•c2≥a2•b+b2•c+c2•a,
即有a3+b3+c3≥a2b+b2c+c2a.
点评 本题考查不等式的证明,考查排序原理:反序和≤乱序和≤同序和的运用,属于中档题.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案
相关题目
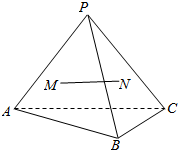 在三棱锥P-ABC中,M,N是△PAB与△PBC的重心,求证:MN∥平面ABC.
在三棱锥P-ABC中,M,N是△PAB与△PBC的重心,求证:MN∥平面ABC.