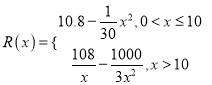题目内容
【题目】已知函数![]() .
.
(1)若![]() ,求函数
,求函数![]() 的极值;
的极值;
(2)设函数![]() ,求函数
,求函数![]() 的单调区间;
的单调区间;
(3)若在区间![]() 上不存在
上不存在![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)极小值为![]() ;(2)见解析(3)
;(2)见解析(3)![]()
【解析】试题分析:(1)先求函数导数,再求导函数零点,列表分析导函数符号变化规律,最后根据符号变化规律确定极值(2)先求导数,再因式分解,根据因子符号确定函数单调区间(3)先求命题的否定:区间![]() 上存在一点
上存在一点![]() ,使得
,使得![]() 成立,转化为对应函数最值当
成立,转化为对应函数最值当![]() 时,
时, ![]() ,再根据函数单调性确定函数最值,即得实数
,再根据函数单调性确定函数最值,即得实数![]() 的取值范围.最后根据补集得满足条件的实数
的取值范围.最后根据补集得满足条件的实数![]() 的取值范围.
的取值范围.
试题解析:(I)当![]() 时,
时, ![]() ,列极值分布表
,列极值分布表
![]() 在(0,1)上递减,在
在(0,1)上递减,在![]() 上递增,∴
上递增,∴![]() 的极小值为
的极小值为![]() ;
;
(II)![]()
![]()
①当![]() 时,
时, ![]() 在
在![]() 上递增;
上递增;
②当![]() 时,
时, ![]() ,
,
∴![]() 在
在![]() 上递减,在
上递减,在![]() 上递增;
上递增;
(III)先解区间![]() 上存在一点
上存在一点![]() ,使得
,使得![]() 成立
成立
![]() 在
在![]() 上有解
上有解![]() 当
当![]() 时,
时, ![]()
由(II)知
①当![]() 时,
时, ![]() 在
在![]() 上递增,
上递增, ![]() ∴
∴![]()
②当![]() 时,
时, ![]() 在
在![]() 上递减,在
上递减,在![]() 上递增
上递增
当![]() 时,
时, ![]() 在
在![]() 上递增,
上递增, ![]()
![]() 无解
无解
当![]() 时,
时, ![]() 在
在![]() 上递减
上递减
![]() ,∴
,∴![]() ;
;
当![]() 时,
时, ![]() 在
在![]() 上递减,在
上递减,在![]() 上递增
上递增
![]()
令![]() ,则
,则![]()
![]() 在
在![]() 递减,
递减, ![]() ,
, ![]() 无解,
无解,
即![]() 无解;
无解;
综上:存在一点![]() ,使得
,使得![]() 成立,实数
成立,实数![]() 的取值范围为:
的取值范围为: ![]() 或
或![]() .
.
所以不存在一点![]() ,使得
,使得![]() 成立,实数
成立,实数![]() 的取值范围为
的取值范围为![]() .
.

 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案【题目】在对人们休闲方式的一次调查中,共调查120人,其中女性70人,男性50人.女性中有40人主要的休闲方式是看电视,另外30人主要的休闲方式是运动;男性中有20人主要的休闲方式是看电视,另外30人主要的休闲方式是运动.
(1)根据以上数据建立一个2×的列联表:
休闲方式 性别 | 看电视 | 运 动 | 总 计 |
女 性 | |||
男 性 | |||
总 计 |
(2)有多大的把握认为休闲方式与性别有关?
参考公式及数据:K2=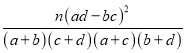
①当K2>2.706时,有90%的把握认为A、B有关联;
②当K2>3.841时,有95%的把握认为A、B有关联;
③当K2>6.635时,有99%的把握认为A、B有关联.