题目内容
 选修4-1:几何证明选讲
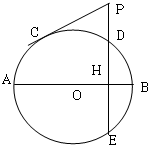
选修4-1:几何证明选讲如图,AB为圆O的直径,BE为圆O的切线,点C为圆O上不同于A、B的一点,AD为∠BAC的平分线,且分别与BC交于H,与圆O交于D,与BE交于E,连结BD、CD.
(Ⅰ)求证:∠DBE=∠DBC
(Ⅱ)若EH=BE=a,求AH.
分析:(I)由AD为∠BAC的平分线得
=
,得出∠DBC=∠BCD,再由弦切角定理得到∠DBE=∠BCD,可得∠DBE=∠DBC;
(II)根据AB为圆O的直径得BD⊥AD,在△BEH利用“三线合一”证出BH=BE,结合EH=BE=a,得到△BEH是边长为a的等边三角形,可得∠E=60°.最后在Rt△ABE中利用三角函数的定义算出AE=2BE=2a,从而可得AH=AE-EH=a.
 |
| BD |
 |
| CD |
(II)根据AB为圆O的直径得BD⊥AD,在△BEH利用“三线合一”证出BH=BE,结合EH=BE=a,得到△BEH是边长为a的等边三角形,可得∠E=60°.最后在Rt△ABE中利用三角函数的定义算出AE=2BE=2a,从而可得AH=AE-EH=a.
解答: 解:(I)∵AD为∠BAC的平分线,即∠DAB=∠DAC,
解:(I)∵AD为∠BAC的平分线,即∠DAB=∠DAC,
∴
=
,可得∠DBC=∠BCD,
又∵BE与圆O相切于点B,
∴∠DBE=∠BCD,可得∠DBE=∠DBC;
(II)∵AB为圆O的直径,∴BD⊥AD,
又∵△BEH中,∠DBE=∠DBC,BD⊥EH,∴BH=BE,
∵EH=BE=a,∴△BEH是边长为a的等边三角形,可得∠E=60°,
因此Rt△ABE中,cos∠E=
=
,可得AE=2BE=2a,
∴AH=AE-EH=a.
 解:(I)∵AD为∠BAC的平分线,即∠DAB=∠DAC,
解:(I)∵AD为∠BAC的平分线,即∠DAB=∠DAC,∴
 |
| BD |
 |
| CD |
又∵BE与圆O相切于点B,
∴∠DBE=∠BCD,可得∠DBE=∠DBC;
(II)∵AB为圆O的直径,∴BD⊥AD,
又∵△BEH中,∠DBE=∠DBC,BD⊥EH,∴BH=BE,
∵EH=BE=a,∴△BEH是边长为a的等边三角形,可得∠E=60°,
因此Rt△ABE中,cos∠E=
| BE |
| AB |
| 1 |
| 2 |
∴AH=AE-EH=a.
点评:本题给出圆的直径与切线,求证角相等并求线段的长.着重考查了圆的直径的性质、等腰三角形的判定与性质、圆周角定理与弦切角定理等知识,属于中档题.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
 选修4-1:几何证明选讲
选修4-1:几何证明选讲 A、选修4-1:几何证明选讲
A、选修4-1:几何证明选讲  选修4-1:几何证明选讲
选修4-1:几何证明选讲 (2012•徐州模拟)选修4-1:几何证明选讲
(2012•徐州模拟)选修4-1:几何证明选讲 (2013•南京二模)选修4-1:几何证明选讲
(2013•南京二模)选修4-1:几何证明选讲