题目内容
设正整数数列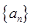 满足:
满足: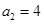 ,且对于任何
,且对于任何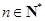 ,有
,有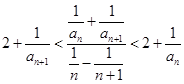 .
.
(1)求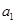 ,
,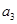 ;
;
(2)求数列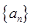 的通项
的通项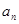 .
.
(1) 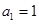 ,
,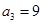 ;(2)
;(2) 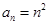 .
.
解析试题分析:(1)令 ,根据
,根据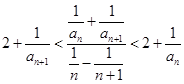 算得
算得 ,再根据
,再根据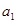 是正整数,算得.
是正整数,算得.
当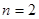 时,同样根据
时,同样根据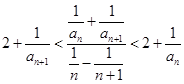 ,将
,将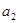 代入,得到
代入,得到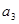 的范围,根据
的范围,根据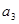 是正整数,求得
是正整数,求得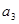 .
.
(2)先根据 可猜想
可猜想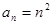 ,再用数学归纳法证明.
,再用数学归纳法证明.
试题解析:解:(1)据条件得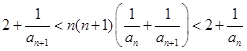 ①
①
当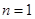 时,由
时,由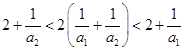 ,即有
,即有 ,
,
解得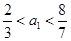 .因为
.因为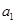 为正整数,故
为正整数,故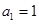 .
.
当 时,由
时,由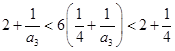 ,
,
解得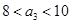 ,所以
,所以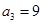 .
.
(2)方法一:由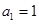 ,
,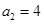 ,
,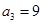 ,猜想:
,猜想: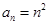 .
.
下面用数学归纳法证明.
1 当
当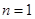 ,
,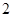 时,由(1)知
时,由(1)知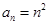 均成立;
均成立;
2 假设
假设 成立,则
成立,则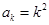 ,则
,则 时
时
由①得
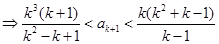
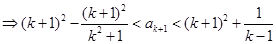
因为 时,
时, ,所以
,所以 .
. ,所以
,所以 .
.
又 ,所以
,所以 .
.
故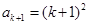 ,即
,即 时,
时,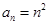 成立.
成立.
由1 ,2
,2 知,对任意
知,对任意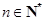 ,
,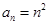 .
.
(2)方法二:
由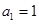 ,
,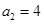 ,
,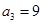 ,猜想:
,猜想: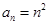 .
.
下面用数学归纳法证明.
1 当
当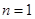 ,
,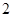 时,由(1)知
时,由(1)知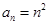 均成立;
均成立;
2 假设
假设 成立,则
成立,则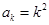 ,则
,则 时
时
由①得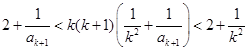
即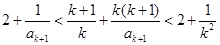 ②
②
由②左式,得 ,即
,即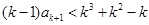 ,因为两端为整数,
,因为两端为整数,
则 .于是
.于是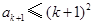 ③
③
又由②右式,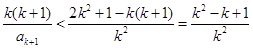 .
.
则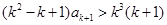 .
.
因为两端为正整数,则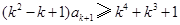 ,
,
所以
练习册系列答案
相关题目
 的前
的前 项和为
项和为 ,且
,且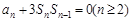 ,
,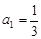 .
.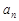 ;
;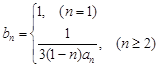 ,设
,设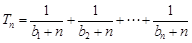 ,若
,若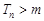 对
对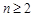 恒成立,求实数
恒成立,求实数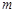 的取值范围.
的取值范围.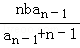 (n≥2)
(n≥2)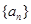 的首项
的首项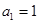 ,公差
,公差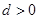 ,且第
,且第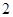 项、第
项、第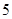 项、第
项、第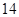 项分别是等比数列
项分别是等比数列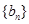 的第
的第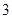 项、第
项、第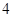 项.
项.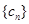 对
对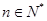 ,均有
,均有 成立,求
成立,求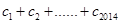 .
.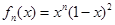 在
在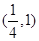 上的最大值为
上的最大值为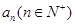
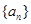 的通项公式;
的通项公式;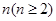 ,都有
,都有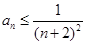 ;
;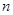 项和
项和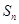 ,求证:对任何正整数
,求证:对任何正整数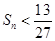 成立
成立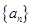 是首项为
是首项为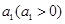 ,公差为
,公差为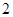 的等差数列,其前
的等差数列,其前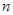 项和为
项和为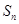 ,且
,且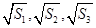 成等差数列.
成等差数列.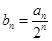 的前
的前 ,求
,求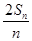 =an+1-
=an+1- n2-n-
n2-n-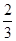 ,n∈N*.
,n∈N*.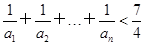 .
.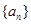 的首项
的首项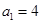 ,公差
,公差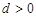 ,且
,且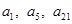 分别是正数等比数列
分别是正数等比数列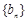 的
的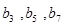 项.
项.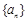 与
与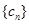 对任意
对任意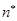 均有
均有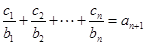 成立,设
成立,设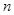 项和为
项和为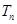 ,求
,求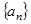 的各项均是正数,其前
的各项均是正数,其前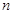 项和为
项和为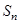 ,满足
,满足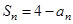 .
.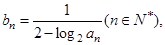 数列
数列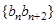 的前
的前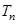 ,求证:
,求证: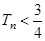 .
.