题目内容
设函数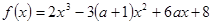 ,其中
,其中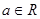 .
.
(1)若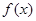 在
在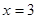 处取得极值,求常数
处取得极值,求常数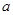 的值;
的值;
(2)设集合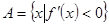 ,
,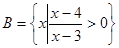 ,若
,若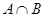 元素中有唯一的整数,求
元素中有唯一的整数,求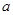 的取值范围.
的取值范围.
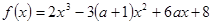 ,其中
,其中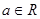 .
. (1)若
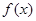 在
在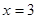 处取得极值,求常数
处取得极值,求常数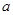 的值;
的值;(2)设集合
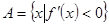 ,
,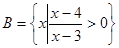 ,若
,若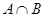 元素中有唯一的整数,求
元素中有唯一的整数,求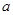 的取值范围.
的取值范围.(1)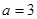 ; (2)
; (2)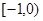
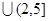
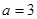 ; (2)
; (2)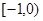
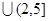
试题分析:(1)由
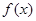 在
在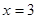 处取得极值,可得
处取得极值,可得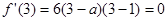 从而解得
从而解得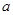 ,此问注意结合极值定义检验所求
,此问注意结合极值定义检验所求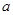 值是否为极值点;(2)分
值是否为极值点;(2)分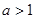 ,
,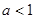 ,和
,和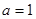 三种情况得出集合A,然后由
三种情况得出集合A,然后由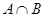 元素中有唯一的整数,分析端点,从而求出
元素中有唯一的整数,分析端点,从而求出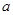 的取值范围.
的取值范围.试题解析:(1)
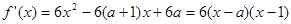 ,又
,又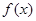 在
在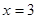 处取得极值,故
处取得极值,故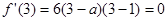 ,解得
,解得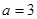 .经检验知当
.经检验知当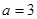 时,
时,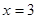 为
为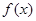 的极值点,故
的极值点,故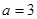 .
.(2)
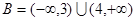 ,
,当
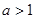 时,
时,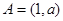 ,则该整数为2,结合数轴可知
,则该整数为2,结合数轴可知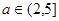 ,
,当
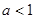 时,
时,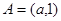 ,则该整数为0,结合数轴可知
,则该整数为0,结合数轴可知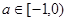
当
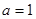 时,
时,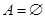 ,不合条件.
,不合条件.综上述,
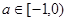
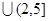 .
.
练习册系列答案
相关题目
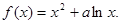
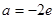 时,求函数
时,求函数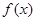 的单调区间和极值;
的单调区间和极值;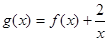 在[1,4]上是减函数,求实数
在[1,4]上是减函数,求实数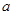 的取值范围.
的取值范围. ,
,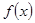 的极值点;
的极值点;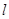 过点
过点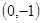 ,并且与曲线
,并且与曲线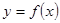 相切,求直线
相切,求直线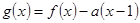 ,其中
,其中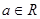 ,求函数
,求函数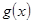 在
在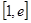 上的最小值(其中
上的最小值(其中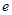 为自然对数的底数).
为自然对数的底数).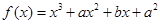 .在
.在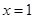 处有极值10,则
处有极值10,则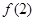 等于_______.
等于_______.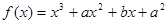 在
在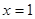 处有极值
处有极值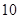 ,则
,则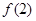 等于( )
等于( )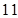 或
或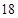
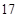 或18
或18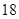
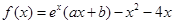 ,曲线
,曲线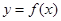 在点
在点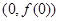 处切线方程为
处切线方程为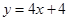 。
。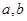 的值;
的值;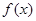 的单调性,并求
的单调性,并求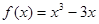
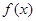 的单调区间;
的单调区间;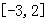 上的最值.
上的最值.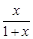 .
.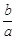 .
.