题目内容
(12分)在平面直角坐标系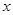 O
O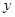 中,直线
中,直线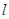 与抛物线
与抛物线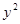 =2
=2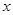 相交于A、B两点.
相交于A、B两点.
(Ⅰ)求证:命题“如果直线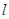 过点T(3,0),那么
过点T(3,0),那么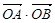 =3”是真命题;
=3”是真命题;
(Ⅱ)写出(1)中命题的逆命题,判断它是真命题还是假命题,并说明理由.
(1)见解析
(2)逆命题是:“设直线l交抛物线y2=2x于A、B两点,如果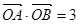 ,那么该直线过点T(3,0).”该命题是假命题.
,那么该直线过点T(3,0).”该命题是假命题.
解析试题分析:(I)直线方程与抛物线方程联立,消去x后利用韦达定理判断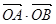 =x1x2+y1y2=
=x1x2+y1y2=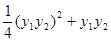 的值是否为3,从而确定此命题是否为真命题.
的值是否为3,从而确定此命题是否为真命题.
(II)根据四种命题之间的关系写出该命题的逆命题,然后再利用直线与抛物线的位置关系知识来判断其真假.
证明:(1)解法一:设过点T(3,0)的直线l交抛物线y2=2x于点A(x1,y1)、B(x2,y2).
当直线l的钭率不存在时,直线l的方程为x=3,此时,直线l与抛物线相交于
A(3,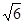 )、B(3,-
)、B(3,-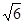 ),∴
),∴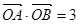 =3.
=3.
当直线l的钭率存在时,设直线l的方程为y=k(x-3),其中k≠0.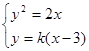 得ky2-2y-6k=0,则y1y2=-6. 又∵x1=
得ky2-2y-6k=0,则y1y2=-6. 又∵x1=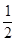 y12, x2=
y12, x2=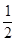 y22,
y22,
∴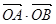 =x1x2+y1y2=
=x1x2+y1y2=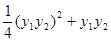 ="3." 综上所述, 命题“......”是真命题.
="3." 综上所述, 命题“......”是真命题.
解法二:设直线l的方程为my=x-3与y2="2x" 联立得到y2-2my-6=0 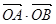 =x1x2+y1y2
=x1x2+y1y2
=(my1+3) (my2+3)+ y1y2=(m2+1) y1y2+3m(y1+y2)+9=(m2+1)× (-6)+3m×2m+9=3
(2)逆命题是:“设直线l交抛物线y2=2x于A、B两点,如果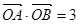 ,那么该直线过点T(3,0).”该命题是假命题. 例如:取抛物线上的点A(2,2),B(
,那么该直线过点T(3,0).”该命题是假命题. 例如:取抛物线上的点A(2,2),B(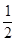 ,1),此时
,1),此时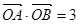 =3,
=3,
直线AB的方程为y=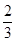 (x+1),而T(3,0)不在直线AB上.
(x+1),而T(3,0)不在直线AB上.
考点:四种命题之间的关系,直线与抛物线的位置关系,向量的数量积.
点评:本小题本质是以四种命题的关系为知识载体主要考查直线与抛物线的位置关系.由抛物线y2=2x上的点A(x1,y1)、B(x2,y2)满足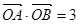 ,可得y1y2=-6.或y1y2=2,如果y1y2=-6,可证得直线AB过点(3,0);如果y1y2="2," 可证得直线AB过点(-1,0),而不过点(3,0).
,可得y1y2=-6.或y1y2=2,如果y1y2=-6,可证得直线AB过点(3,0);如果y1y2="2," 可证得直线AB过点(-1,0),而不过点(3,0).

 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案 均在椭圆
均在椭圆 上,直线
上,直线 分别过椭圆的左、右焦点
分别过椭圆的左、右焦点 当
当 时,有
时,有
 的方程
的方程 是椭圆
是椭圆 为圆
为圆 的任一条直径,求
的任一条直径,求 的最大值
的最大值 的左,右焦点分别为
的左,右焦点分别为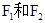 ,过
,过 的直线L与椭圆C相交 A,B于两点,且直线L的倾斜角为
的直线L与椭圆C相交 A,B于两点,且直线L的倾斜角为 ,点
,点 到直线L的距离为
到直线L的距离为 ,
, 求椭圆C的方程.(12分)
求椭圆C的方程.(12分) ,左右焦点分别为
,左右焦点分别为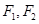 ,
, 上一点
上一点 满足
满足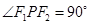 ,求
,求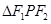 的面积;
的面积; 交
交 ,线段
,线段 的中点为
的中点为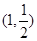 ,求直线
,求直线 :
: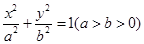 的两个焦点为
的两个焦点为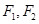 ,点
,点 在椭圆
在椭圆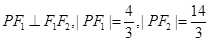 .
.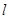 过圆
过圆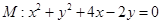 的圆心,交椭圆
的圆心,交椭圆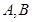 两点,且
两点,且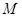 对称,求直线
对称,求直线 的离心率为2,坐标原点到直线AB的距离为
的离心率为2,坐标原点到直线AB的距离为 ,其中A
,其中A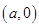 ,B
,B .
.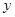 轴正半轴上的端点,过B1作直线与双曲线交于
轴正半轴上的端点,过B1作直线与双曲线交于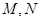 两点,求
两点,求 时,直线
时,直线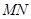 的方程.
的方程. 与平面上两定点
与平面上两定点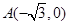 、
、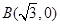 连线的斜率的积为定
连线的斜率的积为定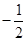 .
.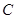 ;(2)设直线
;(2)设直线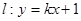 与曲线
与曲线 、
、 两点,当|
两点,当| |=
|= 时,求直线
时,求直线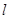 的方程.
的方程. 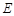 的普通方程为
的普通方程为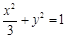
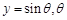 为参数,求椭圆
为参数,求椭圆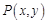 是椭圆
是椭圆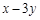 的取值范围.
的取值范围. 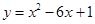 与坐标轴的交点都在圆上.
与坐标轴的交点都在圆上. 交于A,B两点,且
交于A,B两点,且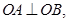 求a的值.
求a的值.