题目内容
在四面体ABCD中,E,F分别是AC,BD的中点,若AB=2,CD=4,EF⊥AB,则AB与CD所成的角的度数为( )
分析:取BC得中点G,则由题意及三角形的中位线的性质可得EG平行且等于
AB,FG平行且等于
CD,故∠EGF(或其补角)即为所求.再由AB=2,CD=4,EF⊥AB,可得EF⊥EG,且EG=
AB=1,FG=
CD=2.再利用直角三角形中边角关系求得cos∠EGF=
=
,从而求得∠EGF的大小.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| EG |
| FG |
| 1 |
| 2 |
解答:解:取BC得中点G,则由题意及三角形的中位线的性质可得EG平行且等于
AB,
FG平行且等于
CD,故∠EGF(或其补角)即为所求.
再由AB=2,CD=4,EF⊥AB,可得EF⊥EG,且EG=
AB=1,FG=
CD=2.
直角三角形EFG中,cos∠EGF=
=
,
∴∠EGF=60°,
故选 C.
| 1 |
| 2 |
FG平行且等于
| 1 |
| 2 |
再由AB=2,CD=4,EF⊥AB,可得EF⊥EG,且EG=
| 1 |
| 2 |
| 1 |
| 2 |
直角三角形EFG中,cos∠EGF=
| EG |
| FG |
| 1 |
| 2 |
∴∠EGF=60°,
故选 C.
点评:本题主要考查异面直线所成的角的定义,体现了转化的数学思想,属于中档题.

练习册系列答案
相关题目
在四面体ABCD中,设AB=1,CD=2且AB⊥CD,若异面直线AB与CD间的距离为2,则四面体ABCD的体积为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 在四面体ABCD中,M、N分别是面△ACD、△BCD的重心,则四面体的四个面中与MN平行的是
在四面体ABCD中,M、N分别是面△ACD、△BCD的重心,则四面体的四个面中与MN平行的是 将图1中的等腰直角三角形ABC沿斜边BC的中线折起得到四面体ABCD(如图2),则在四面体ABCD中,AD与BC的位置关系是( )
将图1中的等腰直角三角形ABC沿斜边BC的中线折起得到四面体ABCD(如图2),则在四面体ABCD中,AD与BC的位置关系是( )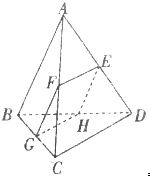 如图,在四面体ABCD中,截面EFGH平行于对棱AB和CD,且FG⊥GH,试问截面在什么位置时其截面面积最大.
如图,在四面体ABCD中,截面EFGH平行于对棱AB和CD,且FG⊥GH,试问截面在什么位置时其截面面积最大.