题目内容
在四面体ABCD中,已知∠ADB=∠BDC=∠CDA=60°,AD=BD=3,CD=2,则四面体ABCD的外接球的半径为
.
| 3 |
| 3 |
分析:设四面体ABCD的外接球球心为O,则O在过△ABD的外心N且垂直于平面ABD的垂线上,且点N为△ABD的中心.设P,M分别为AB,CD的中点,则N在DP上,且ON⊥DP,OM⊥CD,从而可求DM,MN,进而可求四边形DMON的外接圆的直径,即可求得球O的半径.
解答: 解:设四面体ABCD的外接球球心为O,则O在过△ABD的外心N且垂直于平面ABD的垂线上.
解:设四面体ABCD的外接球球心为O,则O在过△ABD的外心N且垂直于平面ABD的垂线上.
由题设知,△ABD是正三角形,则点N为△ABD的中心.
设P,M分别为AB,CD的中点,则N在DP上,且ON⊥DP,OM⊥CD.
因为∠CDA=∠CDB=∠ADB=60°,设CD与平面ABD所成角为θ,
∴cosθ=
,sinθ=
.
在△DMN中,DM=
CD=1,DN=
•DP=
•
•3=
.
由余弦定理得MN2=12+(
)2-2•1•
•
=2,
故MN=
.
∴四边形DMON的外接圆的直径OD=
=
=
.
故球O的半径R=
.
故答案为:
 解:设四面体ABCD的外接球球心为O,则O在过△ABD的外心N且垂直于平面ABD的垂线上.
解:设四面体ABCD的外接球球心为O,则O在过△ABD的外心N且垂直于平面ABD的垂线上.由题设知,△ABD是正三角形,则点N为△ABD的中心.
设P,M分别为AB,CD的中点,则N在DP上,且ON⊥DP,OM⊥CD.
因为∠CDA=∠CDB=∠ADB=60°,设CD与平面ABD所成角为θ,
∴cosθ=
| 1 | ||
|
| ||
|
在△DMN中,DM=
| 1 |
| 2 |
| 2 |
| 3 |
| 2 |
| 3 |
| ||
| 2 |
| 3 |
由余弦定理得MN2=12+(
| 3 |
| 3 |
| 1 | ||
|
故MN=
| 2 |
∴四边形DMON的外接圆的直径OD=
| MN |
| sinθ |
| ||||||
|
| 3 |
故球O的半径R=
| 3 |
故答案为:
| 3 |
点评:本题考查四面体ABCD的外接球,考查学生的计算能力,确定四面体ABCD的外接球球心位置是关键.

练习册系列答案
相关题目
在四面体ABCD中,设AB=1,CD=2且AB⊥CD,若异面直线AB与CD间的距离为2,则四面体ABCD的体积为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
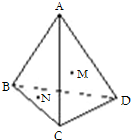 在四面体ABCD中,M、N分别是面△ACD、△BCD的重心,则四面体的四个面中与MN平行的是
在四面体ABCD中,M、N分别是面△ACD、△BCD的重心,则四面体的四个面中与MN平行的是 将图1中的等腰直角三角形ABC沿斜边BC的中线折起得到四面体ABCD(如图2),则在四面体ABCD中,AD与BC的位置关系是( )
将图1中的等腰直角三角形ABC沿斜边BC的中线折起得到四面体ABCD(如图2),则在四面体ABCD中,AD与BC的位置关系是( )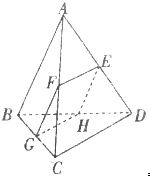 如图,在四面体ABCD中,截面EFGH平行于对棱AB和CD,且FG⊥GH,试问截面在什么位置时其截面面积最大.
如图,在四面体ABCD中,截面EFGH平行于对棱AB和CD,且FG⊥GH,试问截面在什么位置时其截面面积最大.