题目内容
在四面体ABCD中,设AB=1,CD=2且AB⊥CD,若异面直线AB与CD间的距离为2,则四面体ABCD的体积为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
分析:由已知中AB⊥CD,我们可以过AB做一个平面α与CD垂直,则四面体ABCD的体积可转化为:两个以“平面α截四面体ABCD所得截面”为底,高之和为CD的两个小四面体的和,代入棱锥体积公式,即可得到答案.
解答:解:∵AB垂直于CD,
∴可以做一包含AB的平面α,
使平面α与线段CD垂直.
这样α将四面体剖成两个小的四面体.
将截面视为底,CD视为两个四面体高的总和,
那么两个小四面体的体积之和即为四面体ABCD的体积:
V=
×(
×2×1)×2=
故选C
∴可以做一包含AB的平面α,
使平面α与线段CD垂直.
这样α将四面体剖成两个小的四面体.
将截面视为底,CD视为两个四面体高的总和,
那么两个小四面体的体积之和即为四面体ABCD的体积:
V=
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
故选C
点评:本题考查的知识点是棱柱、棱锥、棱台的体积公式,其中过AB做一个平面α与CD垂直,将四面体ABCD的体积转化为,两个小四面体的体积之和,是解答本题的关键.

练习册系列答案
 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
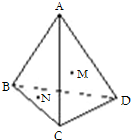 在四面体ABCD中,M、N分别是面△ACD、△BCD的重心,则四面体的四个面中与MN平行的是
在四面体ABCD中,M、N分别是面△ACD、△BCD的重心,则四面体的四个面中与MN平行的是 将图1中的等腰直角三角形ABC沿斜边BC的中线折起得到四面体ABCD(如图2),则在四面体ABCD中,AD与BC的位置关系是( )
将图1中的等腰直角三角形ABC沿斜边BC的中线折起得到四面体ABCD(如图2),则在四面体ABCD中,AD与BC的位置关系是( )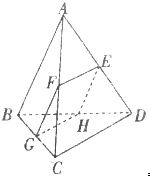 如图,在四面体ABCD中,截面EFGH平行于对棱AB和CD,且FG⊥GH,试问截面在什么位置时其截面面积最大.
如图,在四面体ABCD中,截面EFGH平行于对棱AB和CD,且FG⊥GH,试问截面在什么位置时其截面面积最大.