题目内容
【题目】如图，四棱锥P-ABCD中，侧面PAD为等边三角形且垂直于底面ABCD，AB=BC=
AD,∠BAD=∠ABC=90°，E是PD的中点．
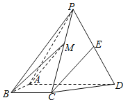
（1）证明：直线CE∥平面PAB；
（2）点M在棱PC上，且直线BM与底面ABCD所成角为45°，求二面角M-AB-D的余弦值．
【答案】（1）见解析（2）
【解析】
（1）取PA的中点F，连接EF，BF，通过证明CE∥BF，利用直线与平面平行的判定定理证明即可．
（2）利用已知条件转化求解M到底面的距离，作出二面角的平面角，然后求解二面角M-AB-D的余弦值即可．
（1）证明：取PA的中点F，连接EF，BF，因为E是PD的中点，所以EF
AD,EF=
AD，AB=BC=AD，∠BAD=∠ABC=90°，∴BCEF, BC=EF
∴BCEF是平行四边形，可得CE∥BF，BF平面PAB，CE平面PAB，
∴直线CE平面PAB；
（2）解：四棱锥P-ABCD中，侧面PAD为等边三角形且垂直于底面ABCD，AB=BC=AD，∠BAD=∠ABC=90°，E是PD的中点．
取AD的中点O，M在底面ABCD上的射影N在OC上，设AD=2，则AB=BC=1，OP=
，
∴∠PCO=60°，直线BM与底面ABCD所成角为45°，
可得：BN=MN，CN=
MN，BC=1，可得：1+
BN2=BN2，BN=
，MN=，
作NQ⊥AB于Q，连接MQ，AB⊥MN，所以∠MQN就是二面角M-AB-D的平面角，MQ=
=
，二面角M-AB-D的余弦值为：
=．
【题目】目前，学案导学模式已经成为教学中不可或缺的一部分，为了了解学案的合理使用是否对学生的期末复习有着重要的影响，我校随机抽取100名学生，对学习成绩和学案使用程度进行了调查，统计数据如表所示：
善于使用学案 | 不善于使用学案 | 总计 | |
学习成绩优秀 | 40 | ||
学习成绩一般 | 30 | ||
总计 | 100 |
参考公式： 
，其中n=a+b+c+d．
参考数据：
P（K2≥k0） | 0.050 | 0.010 | 0.001 |
k0 | 3.841 | 6.635 | 10.828 |
已知随机抽查这100名学生中的一名学生，抽到善于使用学案的学生概率是0.6．
（1）请将上表补充完整（不用写计算过程）；
（2）试运用独立性检验的思想方法分析：有多大的把握认为学生的学习成绩与对待学案的使用态度有关？
（3）利用分层抽样的方法从善于使用学案的同学中随机抽取6人，从这6人中抽出3人继续调查，设抽出学习成绩优秀的人数为X，求X的分布列和数学期望．
