题目内容
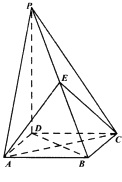
【题目】已知正四棱柱ABCD﹣A1B1C1D1（底面是正方形，侧棱垂直于底面）的8个顶点都在球O的表面上，AB=1，AA1′=2，则球O的半径R=；若E，F是棱AA1和DD1的中点，则直线EF被球O截得的线段长为 ． 
【答案】6π；
【解析】解：正四棱柱对角线为球直径，A1C2=1+1+4，
所以R= 
，所以球的表面积为6π；
由已知所求EF是正四棱柱在球中其中一个截面的直径上的一部分，Q为EF的中点，
d= 
，R= ，所以PQ= 
= 
，
所以2PQ= ．
所以答案是：6π； 
【考点精析】认真审题，首先需要了解棱柱的结构特征(两底面是对应边平行的全等多边形；侧面、对角面都是平行四边形；侧棱平行且相等；平行于底面的截面是与底面全等的多边形)．
【题目】某企业响应省政府号召，对现有设备进行改造，为了分析设备改造前后的效果，现从设备改造前后生产的大量产品中各抽取了
件产品作为样本，检测一项质量指标值，若该项质量指标值落在
内的产品视为合格品，否则为不合格品.如图是设备改造前的样本的频率分布直方图，表
是设备改造后的样本的频数分布表.
表：设备改造后样本的频数分布表
质量指标值 |
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
（1）完成下面的
列联表，并判断是否有
的把握认为该企业生产的这种产品的质量指标值与设备改造有关；
设备改造前 | 设备改造后 | 合计 | |
合格品 | |||
不合格品 | |||
合计 |
（2）根据频率分布直方图和表 提供的数据，试从产品合格率的角度对改造前后设备的优劣进行比较；
（3）企业将不合格品全部销毁后，根据客户需求对合格品进行登记细分，质量指标值落在
内的定为一等品，每件售价
元；质量指标值落在
或
内的定为二等品，每件售价
元；其它的合格品定为三等品，每件售价
元.根据表的数据，用该组样本中一等品、二等品、三等品各自在合格品中的频率代替从所有产品中抽到一件相应等级产品的概率.现有一名顾客随机购买两件产品，设其支付的费用为
（单位：元），求的分布列和数学期望.
附：
|
|
|
|
|
|
|
|
|
|
|
|
