��Ŀ����
����Ŀ��ij��ҵ��Ӧʡ�������٣��������豸���и��죬Ϊ�˷����豸����ǰ���Ч�����ִ��豸����ǰ�������Ĵ�����Ʒ�и���ȡ��![]() ����Ʒ��Ϊ���������һ������ָ��ֵ������������ָ��ֵ����
����Ʒ��Ϊ���������һ������ָ��ֵ������������ָ��ֵ����![]() �ڵIJ�Ʒ��Ϊ�ϸ�Ʒ������Ϊ���ϸ�Ʒ.��ͼ���豸����ǰ��������Ƶ�ʷֲ�ֱ��ͼ����
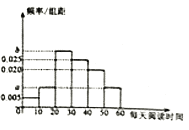
�ڵIJ�Ʒ��Ϊ�ϸ�Ʒ������Ϊ���ϸ�Ʒ.��ͼ���豸����ǰ��������Ƶ�ʷֲ�ֱ��ͼ����![]() ���豸������������Ƶ���ֲ���.
���豸������������Ƶ���ֲ���.

�����豸�����������Ƶ���ֲ���
����ָ��ֵ |
|
|
|
|
|
|
Ƶ�� |
|
|
|
|
|
|
��1����������![]() �����������ж��Ƿ���
�����������ж��Ƿ���![]() �İ�����Ϊ����ҵ���������ֲ�Ʒ������ָ��ֵ���豸�����йأ�
�İ�����Ϊ����ҵ���������ֲ�Ʒ������ָ��ֵ���豸�����йأ�
�豸����ǰ | �豸����� | �ϼ� | |
�ϸ�Ʒ | |||
���ϸ�Ʒ | |||
�ϼ� |
��2������Ƶ�ʷֲ�ֱ��ͼ�ͱ� �ṩ�����ݣ��ԴӲ�Ʒ�ϸ��ʵĽǶȶԸ���ǰ���豸�����ӽ��бȽϣ�
��3����ҵ�����ϸ�Ʒȫ�����ٺ��ݿͻ�����Ժϸ�Ʒ���еǼ�ϸ�֣�����ָ��ֵ����![]() �ڵĶ�Ϊһ��Ʒ��ÿ���ۼ�
�ڵĶ�Ϊһ��Ʒ��ÿ���ۼ�![]() Ԫ������ָ��ֵ����
Ԫ������ָ��ֵ����![]() ��
��![]() �ڵĶ�Ϊ����Ʒ��ÿ���ۼ�
�ڵĶ�Ϊ����Ʒ��ÿ���ۼ�![]() Ԫ�������ĺϸ�Ʒ��Ϊ����Ʒ��ÿ���ۼ�
Ԫ�������ĺϸ�Ʒ��Ϊ����Ʒ��ÿ���ۼ�![]() Ԫ.���ݱ�
Ԫ.���ݱ�![]() �����ݣ��ø���������һ��Ʒ������Ʒ������Ʒ�����ںϸ�Ʒ�е�Ƶ�ʴ�������в�Ʒ�г鵽һ����Ӧ�ȼ���Ʒ�ĸ���.����һ���˿��������������Ʒ������֧���ķ���Ϊ
�����ݣ��ø���������һ��Ʒ������Ʒ������Ʒ�����ںϸ�Ʒ�е�Ƶ�ʴ�������в�Ʒ�г鵽һ����Ӧ�ȼ���Ʒ�ĸ���.����һ���˿��������������Ʒ������֧���ķ���Ϊ![]() ����λ��Ԫ������
����λ��Ԫ������![]() �ķֲ��к���ѧ����.
�ķֲ��к���ѧ����.
����
|
|
|
|
|
|
|
|
|
|
|
|
![]()
���𰸡�(1)�������������� ��![]() �İ�����Ϊ����ҵ���������ֲ�Ʒ������ָ��ֵ���豸�����йء�
�İ�����Ϊ����ҵ���������ֲ�Ʒ������ָ��ֵ���豸�����йء�
(2)�豸��������ܸ��ţ�
(3)�ֲ��м�������![]() .
.
����������������1�������豸����ǰ��������Ƶ�ʷֲ�ֱ��ͼ���豸������������Ƶ���ֲ������![]() �����������
�����������![]() �����ٽ�ֵ�Ƚϼ��ɵý������2������Ƶ�ʷֲ�ֱ��ͼ��Ƶ���ֲ������ɵõ��豸����ǰ��ƷΪ�ϸ�Ʒ�ĸ��ʺ�
�����ٽ�ֵ�Ƚϼ��ɵý������2������Ƶ�ʷֲ�ֱ��ͼ��Ƶ���ֲ������ɵõ��豸����ǰ��ƷΪ�ϸ�Ʒ�ĸ��ʺ�
�豸������ƷΪ�ϸ�Ʒ�ĸ��ʣ��Ӷ��ɵý������3���������![]() ��ȡֵΪ��
��ȡֵΪ��![]() �����ùŵ�����ʹ�ʽ�����ݶ����ظ�������ʹ�ʽ��������������Ӧ�ĸ��ʣ��Ӷ��ɵ÷ֲ��У���������������ʽ�ɵ�
�����ùŵ�����ʹ�ʽ�����ݶ����ظ�������ʹ�ʽ��������������Ӧ�ĸ��ʣ��Ӷ��ɵ÷ֲ��У���������������ʽ�ɵ�![]() ����ѧ����.
����ѧ����.
��⣺��1�������豸����ǰ��������Ƶ�ʷֲ�ֱ��ͼ���豸������������Ƶ���ֲ�����
��������![]() ��������
��������
�豸����ǰ | �豸����� | �ϼ� | |
�ϸ�Ʒ |
|
|
|
���ϸ�Ʒ |
|
|
|
�ϼ� |
|
|
|
��![]() �������е����ݴ��빫ʽ����ã�
�������е����ݴ��빫ʽ����ã�
![]()
��![]() ��
��
����![]() �İ�����Ϊ����ҵ���������ֲ�Ʒ������ָ��ֵ���豸�����йأ�
�İ�����Ϊ����ҵ���������ֲ�Ʒ������ָ��ֵ���豸�����йأ�
��2�������豸����ǰ��������Ƶ�ʷֲ�ֱ��ͼ���豸������������Ƶ���ֲ�����
��֪���豸����ǰ��ƷΪ�ϸ�Ʒ�ĸ���ԼΪ![]()
�豸������ƷΪ�ϸ�Ʒ�ĸ���ԼΪ![]()
�豸������Ʒ�ϸ��ʸ��ߣ���ˣ��豸��������ܸ��ţ�
��3���ɱ� 1 ֪��
һ��Ʒ��Ƶ��Ϊ![]() ���������в�Ʒ������鵽һ��һ��Ʒ�ĸ���Ϊ
���������в�Ʒ������鵽һ��һ��Ʒ�ĸ���Ϊ![]() ��
��
����Ʒ��Ƶ��Ϊ![]() ���������в�Ʒ������鵽һ������Ʒ�ĸ���Ϊ
���������в�Ʒ������鵽һ������Ʒ�ĸ���Ϊ![]() ��
��
����Ʒ��Ƶ��Ϊ![]() ���������в�Ʒ������鵽һ������Ʒ�ĸ���Ϊ
���������в�Ʒ������鵽һ������Ʒ�ĸ���Ϊ![]() .
.
����֪�ã��������![]() ��ȡֵΪ��
��ȡֵΪ��![]() ��
��
![]()
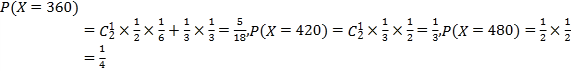
���������![]() �ķֲ���Ϊ��
�ķֲ���Ϊ��
|
|
|
|
|
|
|
|
|
|
|
|
��![]() .
.

����Ŀ��ij���ֽ����г���ij�ͺŵĶ���������ʹ������![]() ��
��![]() �������ۼ۸�
�������ۼ۸�![]() ����λ����Ԫ/���������������õ����µĶ�Ӧ���ݣ�
����λ����Ԫ/���������������õ����µĶ�Ӧ���ݣ�
ʹ������ | 2 | 4 | 6 | 8 | 10 |
���ۼ۸� | 16 | 13 | 9.5 | 7 | 4.5 |
��I������![]() ����
����![]() �Ļع�ֱ�߷���
�Ļع�ֱ�߷���![]() .
.
���ο���ʽ��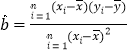 ��
��![]() ��
��
��II����֪ÿ�����ͺ��������չ��۸�Ϊ![]() ��Ԫ�����ݣ�I��������Ļع鷽�̣�Ԥ��
��Ԫ�����ݣ�I��������Ļع鷽�̣�Ԥ��![]() Ϊ��ֵʱ������һ�����ͺ���������õ�����
Ϊ��ֵʱ������һ�����ͺ���������õ�����![]() �������=���ۼ۸�-�չ��۸�
�������=���ۼ۸�-�չ��۸�