题目内容
某车间加工零件的数量 与加工时间
与加工时间 的统计数据如下表:
的统计数据如下表:
零件数 (个) (个) | 10 | 20 | 30 |
加工时间 (分钟) (分钟) | 21 | 30 | 39 |
现已求得上表数据的回归方程
 中的
中的 值为0.9,则据此回归模型可以预测,加工100个零件所需要的加工时间约为( )
值为0.9,则据此回归模型可以预测,加工100个零件所需要的加工时间约为( )A.84分钟 B.94分钟 C.102分钟 D.112分钟
C
解析试题分析:因为 ,又回归直线方程
,又回归直线方程 恒过样本中心点
恒过样本中心点 ,且知
,且知 值为0.9,所以有:
值为0.9,所以有: ,回归直线方程为:
,回归直线方程为: ,从而当
,从而当 时,
时, ,由此可预测:加工100个零件所需要的加工时间约为102分钟,故选C.
,由此可预测:加工100个零件所需要的加工时间约为102分钟,故选C.
考点:线性回归.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
设某大学的女生体重 (单位:
(单位: )与身高
)与身高 (单位:
(单位: )具有线性相关关系,根据一组样本数据
)具有线性相关关系,根据一组样本数据 (
(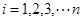 ),用最小二乘法建立的回归方程为
),用最小二乘法建立的回归方程为 ,则下列结论中不正确的是( )
,则下列结论中不正确的是( )
A. 与 与 具有正的线性相关关系 具有正的线性相关关系 |
B.回归直线过样本点的中心 |
C.若该大学某女生身高增加 ,则其体重约增加 ,则其体重约增加 |
D.若该大学某女生身高为 ,则可断定其体重为 ,则可断定其体重为 |
已知样本7,10,14,8,7,12,11,10,8,10,13,10,8,11,8,9,12,9,13,20,那么这组数据落在8.5~11.5的频率为( )
| A.0.5 | B.0.4 | C.0.3 | D.0.2 |
下表提供了某厂节能降耗技术改造后生产某产品过程中记录的产量 (吨)与相应的生产能耗
(吨)与相应的生产能耗 (吨)的几组对应数据. 根据表中提供的数据,求出
(吨)的几组对应数据. 根据表中提供的数据,求出 关于
关于 的线性回归方程是
的线性回归方程是 ,那么表中
,那么表中 的值是( )
的值是( )
 | 3 | 4 | 5 | 6 |
 | 2.5 |  | 4 | 4.5 |
A.
 B.
B. C.
C. D.
D.
一个容量为20的样本,数据的分组及各组的频数如下:
(10,20 ,2;(20,30
,2;(20,30 ,3;(30,40
,3;(30,40 ,4;(40,50
,4;(40,50 ,5;(50,60
,5;(50,60 ,4;(60,70
,4;(60,70 ,2.
,2.
则样本在区间(10,50 上的频率为( )
上的频率为( )
| A.0.5 | B.0.7 | C.0.25 | D.0.05 |
为了了解 名学生的学习情况,采用系统抽样的方法,从中抽取容量为
名学生的学习情况,采用系统抽样的方法,从中抽取容量为 的样本,则分段的间隔为( )
的样本,则分段的间隔为( )
A. | B. | C. | D. |
 ,
, )作平行于
)作平行于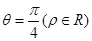 的直线
的直线 ,且
,且 ,则m的值为
,则m的值为 D、6.8
D、6.8  设其平均数为
设其平均数为 ,中位数为
,中位数为 ,众数为
,众数为 ,则有( )
,则有( ) B.
B. C.
C. D.
D.