题目内容
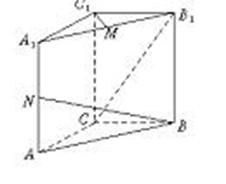
(本题满分12分)如图所示,直三棱柱ABC—A1B1C1中,CA=CB=1,∠BCA=90°,棱AA1=2,M、N分别是A1B1、A1A的中点.
(1)求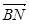 的长; (2)求cos<
的长; (2)求cos< >的值; (3)求证:A1B⊥C1M.
>的值; (3)求证:A1B⊥C1M.
【答案】
(1)|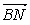 |=
|=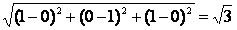 .
.
(2)cos<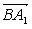 ,
,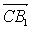 >=
>= .
.
(3)计算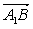 ·
·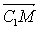 =0,推出A1B⊥C1M。
=0,推出A1B⊥C1M。
【解析】
试题分析:如图,建立空间直角坐标系O—xyz.
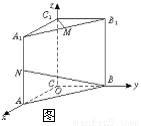
(1)依题意得B(0,1,0)、N(1,0,1)
∴|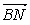 |=
|=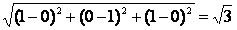 .。。4分
.。。4分
(2)依题意得A1(1,0,2)、B(0,1,0)、C(0,0,0)、B1(0,1,2)
∴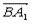 =(1,-1,2),
=(1,-1,2),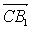 =(0,1,2,),
=(0,1,2,),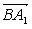 ·
·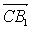 =3,|
=3,|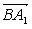 |=
|=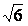 |
|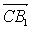 |=
|=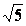
∴cos<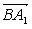 ,
,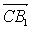 >=
>= .。。。。。。。8分
.。。。。。。。8分
(3)证:依题意,得C1(0,0,2)、M(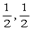 ,2),
,2),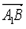 =(-1,1,-2),
=(-1,1,-2),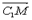 ={
={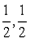 ,0}.∴
,0}.∴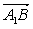 ·
·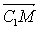 =-
=-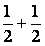 +0=0,∴
+0=0,∴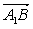 ⊥
⊥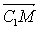 ,∴A1B⊥C1M..。。。。。12分
,∴A1B⊥C1M..。。。。。12分
考点:本题主要考查立体几何中线线垂直,距离及角的计算,空间向量的应用
点评:典型题,立体几何中平行、垂直关系的证明,距离及角的计算问题是高考中的必考题,通过建立适当的坐标系,可使问题简化,向量的坐标运算要准确。

练习册系列答案
相关题目
 为底面的直棱柱被平面
为底面的直棱柱被平面 所截而得.
所截而得.  ,
, 为
为 的中点.
的中点.
 时,求平面
时,求平面 为何值时,在棱
为何值时,在棱 上存在点
上存在点 ,使
,使 平面
平面 中,已知上下两底面为正方形,且边长均为1;侧棱
中,已知上下两底面为正方形,且边长均为1;侧棱 ,为
,为 中点,
中点, 为
为 中点,
中点, 为
为 上一个动点.
上一个动点.
 ;
; 的平
的平
 中,已知
中,已知 的直径
的直径 的中点.
的中点.
 所成角的正弦值.
所成角的正弦值.
