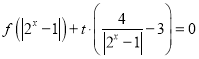Question

【题目】设函数f(x)(m∈R).

（1）当m=1时，求函数的单调区间；

（2）若函数F(x)=f(x)+xm+2有两个零点，求实数m的取值范围.

Answer 1

【答案】(1) 递增区间为(0，e)，递减区间为(e，+∞) (2) (﹣∞，﹣2e).

【解析】

（1）时，求出，求出的解，即可得出结论；

（2）求出整理，有两个零点，转化为函数 有两个零点，求，求出极值点，分析函数值的变化趋势，只需g(x)的极小值g()<0方程有两个零点，解不等式g()<0，即可求出结论.

(1)当m=1时，f(x)，x>0，∴f'(x)，

令f'(x)=0，得1﹣lnx=0，x=e，

随的变化变化如下表：

x	(0，e)	e	(e，+∞)
f'(x)	+	0	﹣
f(x)	递增	极大值	递减

∴函数f(x)的单调递增区间为(0，e)，单调递减区间为(e，+∞)；

(2)F(x)xm+2，定义域为(0，+∞)，

∴F(x)xm+2，

设g(x)=4mlnx+4x2+m2+4mx+8x，

∵函数F(x)=f(x)+xm+2有两个零点，

∴函数g(x)=4mlnx+4x2+m2+4mx+8x有两个零点，

∵g'(x)，

令g'(x)=0得，x，

∵函数g(x)=4mlnx+4x2+m2+4mx+8x有两个零点，

∴函数g(x)在(0，+∞)上不单调，∴0，∴m<0，

随的变化变化如下表：

x	(0，)		(，+∞)
g'(x)	﹣	0	+
g(x)	递减	极小值	递增

∴函数g(x)的极小值为g()，

∵当x→0时，g(x)→+∞；当x→+∞时，g(x)→+∞，

∴若函数g(x)=4mlnx+4x2+m2+4mx+8x有两个零点，

则函数g(x)的极小值g()<0，

即4mln()+4m2﹣4m4m<0，

∴mln()﹣m<0，又∵m<0，∴ln()>1，

∴e，∴m<﹣2e，

∴实数m的取值范围为：(﹣∞，﹣2e).