题目内容
【题目】设f(x)是(﹣∞,+∞)上的奇函数,且f(x+2)=﹣f(x),当0≤x≤1时,f(x)=x.
(1)求f(π)的值;
(2)求﹣1≤x≤3时,f(x)的解析式;
(3)当﹣4≤x≤4时,求f(x)=m(m<0)的所有实根之和.
【答案】
(1)解:∵f(x+2)=﹣f(x),
∴f(x+4)=﹣f(x+2)=f(x),
即函数f(x)是周期为4的周期函数,
则f(π)=f(π﹣4)=﹣f(4﹣π)=﹣(4﹣π)=π﹣4
(2)解:若﹣1≤x≤0,则0≤﹣x≤1,
则f(﹣x)=﹣x,
∵f(x)是奇函数,∴f(﹣x)=﹣x=﹣f(x),
即f(x)=x,﹣1≤x≤0,
即当﹣1≤x≤1时,f(x)=x,
若1≤x≤3,则﹣1≤x﹣2≤1,
∵f(x+2)=﹣f(x),
∴f(x)=﹣f(x﹣2)=﹣(x﹣2)=﹣x+2,
即当﹣1≤x≤3时,f(x)的解析式为f(x)= ![]()
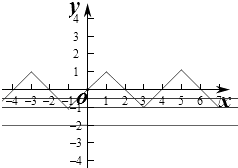
(3)解:作出函数f(x)在﹣4≤x≤4时的图象如图,
则函数的最小值为﹣1,
若m<﹣1,则方程f(x)=m(m<0)无解,
若m=﹣1,则函数在﹣4≤x≤4上的零点为x=﹣1,x=3,则﹣1+3=2,
若﹣1<m<0,则函数在﹣4≤x≤4上共有4个零点,则它们分别关于x=﹣1和x=3对称,
设分别为a,b,c,d,
则a+b=﹣2,b+d=6,
即a+b+c+d=﹣2+6=4.
【解析】(1)由f(x+2)=﹣f(x),可得f(x+4)=﹣f(x+2)=f(x),即f(x)为周期为4的周期函数,即f(π)=π-4,(2)结合分段函数和函数的奇偶性可得出每段的解析式,(3)作出f(x)在﹣4≤x≤4的图像,应用数形结合,根据对称性不难得出所有实根之和为4.
【考点精析】利用函数奇偶性的性质对题目进行判断即可得到答案,需要熟知在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇.
