题目内容
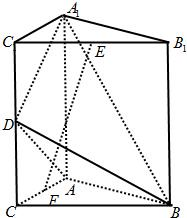 如图,直三棱柱A1B1C1-ABC中,C1C=CB=CA=2,AC⊥CB. D、E分别为棱C1C、B1C1的中点.
如图,直三棱柱A1B1C1-ABC中,C1C=CB=CA=2,AC⊥CB. D、E分别为棱C1C、B1C1的中点.(1)求点E到平面ADB的距离;
(2)求二面角E-A1D-B的平面角的余弦值;
(3)在线段AC上是否存在一点F,使得EF⊥平面A1DB?若存在,确定其位置;若不存在,说明理由.
分析:以CB为x轴,CA为y轴,CC1为z轴,建立空间直角坐标系,则C(0,0,0),A(0,2,0),B(2,0,0),D(0,0,1),E(1,0,2).这种解法的好处就是:(1)解题过程中较少用到空间几何中判定线线、面面、线面相对位置的有关定理,因为这些可以用向量方法来解决.(2)即使立体感稍差一些的学生也可以顺利解出,因为只需画个草图以建立坐标系和观察有关点的位置即可.
(1)
=(2,-2,0),
=(0,-2,1),
=(1,0,1),设平面ADB的法向量为
=(x,y,1)得:可取法向量为
=(1,1,2),则点E到平面ADB的距离d=|
|=
.
(2)A1(0,2,2),E(1,0,2),D(0,0,1)可得
=(1,-2,0),
=(0,-2,-1),
设平面A1ED的法向量为
=(x,y,1),则
=(2,1,-2),平面A1BD的法向量为
=(x,y,1),则
=(1,-1,2),
所以cos<
,
>=
=-
,即求二面角E-A1D-B的余弦值为
.
(3)假设存在点F,坐标为(0,y,0),则
=(-1,y,-2),EF⊥平面A1DB得
∥
,F(0,1,0),F即为AC中点.
(1)
| AB |
| AD |
| DE |
| n |
| n |
| ||||
|
|
| ||
| 2 |
(2)A1(0,2,2),E(1,0,2),D(0,0,1)可得
| A1E |
| A1D |
设平面A1ED的法向量为
| n1 |
| n1 |
| n2 |
| n2 |
所以cos<
| n1 |
| n2 |
| ||||
|
|
| ||
| 6 |
| ||
| 6 |
(3)假设存在点F,坐标为(0,y,0),则
| EF |
| EF |
| n2 |
解答:解:(1)如图所示,以CB为x轴,CA为y轴,CC1为z轴建立空间直角坐标系,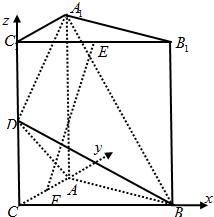 由C1C=CB=CA=2可得C(0,0,0),A(0,2,0),B(2,0,0),D(0,0,1),E(1,0,2).
由C1C=CB=CA=2可得C(0,0,0),A(0,2,0),B(2,0,0),D(0,0,1),E(1,0,2).
则
=(2,-2,0),
=(0,-2,1),
=(1,0,1)
设平面ADB的法向量为
=(x,y,1)得
?
即
=(
,
,1)
则取法向量为
=(1,1,2),
则点E到平面ADB的距离d=|
|=
.(3分)
(2)A1(0,2,2),E(1,0,2),D(0,0,1)
可得
=(1,-2,0),
=(0,-2,-1),
设平面A1ED的法向量为
=(x,y,1)?
?
,
故可令
=(2,1,-2),A1(0,2,2),D(0,0,1),B(2,0,0),
可得
=(0,-2,-1),
=(2,-2,-2),
设平面A1BD的法向量为
=(x,y,1)?
?
,
故可令
=(1,-1,2),
∴cos<
,
>=
=-
,
即求二面角E-A1D-B的余弦值为
;(6分)
(3)假设存在点F,坐标为(0,y,0),
则
=(-1,y,-2),
EF⊥平面A1DB得
∥
,即
=
=
?y=1,
∴F(0,1,0)F即为AC中点.(10分)
 由C1C=CB=CA=2可得C(0,0,0),A(0,2,0),B(2,0,0),D(0,0,1),E(1,0,2).
由C1C=CB=CA=2可得C(0,0,0),A(0,2,0),B(2,0,0),D(0,0,1),E(1,0,2).则
| AB |
| AD |
| DE |
设平面ADB的法向量为
| n |
|
|
| n |
| 1 |
| 2 |
| 1 |
| 2 |
则取法向量为
| n |
则点E到平面ADB的距离d=|
| ||||
|
|
| ||
| 2 |
(2)A1(0,2,2),E(1,0,2),D(0,0,1)
可得
| A1E |
| A1D |
设平面A1ED的法向量为
| n1 |
|
|
故可令
| n1 |
可得
| A1D |
| A1B |
设平面A1BD的法向量为
| n2 |
|
|
故可令
| n2 |
∴cos<
| n1 |
| n2 |
| ||||
|
|
| ||
| 6 |
即求二面角E-A1D-B的余弦值为
| ||
| 6 |
(3)假设存在点F,坐标为(0,y,0),
则
| EF |
EF⊥平面A1DB得
| EF |
| n2 |
| 1 |
| -1 |
| -1 |
| y |
| 2 |
| -2 |
∴F(0,1,0)F即为AC中点.(10分)
点评:本小题考查空间中的线面关系,直线与平面所成的角、点到面的距离、二面角、解三角形等基础知识考查空间想象能力和思维能力.

练习册系列答案
相关题目
 如图在直三棱柱ABC-A1B1C1中∠ACB=90°,AA1=2,AC=BC=1,则异面直线A1B与AC所成角的余弦值是
如图在直三棱柱ABC-A1B1C1中∠ACB=90°,AA1=2,AC=BC=1,则异面直线A1B与AC所成角的余弦值是 如图,直三棱柱ABC-A1B1C1中,∠ACB=90°,M,N分别为A1B,B1C1的中点.
如图,直三棱柱ABC-A1B1C1中,∠ACB=90°,M,N分别为A1B,B1C1的中点. 如图,直三棱柱ABCA1B1C1的底面ABC中,CA=CB=1,∠BCA=90°,棱AA1=2,M、N分别是A1B1、A1A的中点.
如图,直三棱柱ABCA1B1C1的底面ABC中,CA=CB=1,∠BCA=90°,棱AA1=2,M、N分别是A1B1、A1A的中点. (2013•大兴区一模)如图,直三棱柱ABC-A1B1C1中,△ABC是等边三角形,D是BC的中点.
(2013•大兴区一模)如图,直三棱柱ABC-A1B1C1中,△ABC是等边三角形,D是BC的中点. (2013•凉山州二模)如图,直三棱柱ABC-A1B1C1中,AB=AC,BC=2BB1,D为BC中点.
(2013•凉山州二模)如图,直三棱柱ABC-A1B1C1中,AB=AC,BC=2BB1,D为BC中点.