题目内容
14.从一批产品中取出3件产品,设事件A为“三件产品全不是次品”,事件B为“三件产品全是次品”,事件C为“三件产品不全是次品”,则下列结论正确的是( )| A. | 事件B与C互斥 | B. | 事件A与C互斥 | ||
| C. | 任何两个均不互斥 | D. | 任何两个均互斥 |
分析 本题中给了三个事件,四个选项都是研究互斥关系的,可先对每个事件进行分析,再考查四个选项得出正确答案.
解答 解:A为{三件产品全不是次品},指的是三件产品都是正品,B为{三件产品全是次品},
C为{三件产品不全是次品},它包括一件次品,两件次品,三件全是正品三个事件
由此知:A与B是互斥事件,但不对立;A与C是包含关系,不是互斥事件,更不是对立事件;B与C是互斥事件,也是对立事件.
故选:A.
点评 本题考查互斥事件与对立事件,解题的关系是正确理解互斥事件与对立事件,事件的包含等关系且能对所研究的事件所包含的基本事件理解清楚,明白所研究的事件.本题是概念型题.

练习册系列答案
相关题目
4.已知直线$\sqrt{m}$x+$\sqrt{n}$y=4被圆x2+y2=25截得的弦长为6,则直线mx+ny=4与圆(x-1)2+(y-2)2=20的位置关系是( )
| A. | 相离 | B. | 相切 | ||
| C. | 相交且有可能过圆心 | D. | 相交但不过圆心 |
5.一个正方体的顶点都在球面上,它的棱长为1cm,则球的表面积是( )
| A. | 3πcm2 | B. | 12πcm2 | C. | 4πcm2 | D. | 6πcm2 |
2.函数y=$\frac{1}{x}$在x=1到x=2之间的平均变化率为( )
| A. | -1 | B. | -$\frac{1}{2}$ | C. | -2 | D. | 2 |
9. 有两种花色的正六边形地面砖,按下图的规律拼成若干个图案,则第六个图案中有菱形纹的正六边形的个数是( )
有两种花色的正六边形地面砖,按下图的规律拼成若干个图案,则第六个图案中有菱形纹的正六边形的个数是( )
 有两种花色的正六边形地面砖,按下图的规律拼成若干个图案,则第六个图案中有菱形纹的正六边形的个数是( )
有两种花色的正六边形地面砖,按下图的规律拼成若干个图案,则第六个图案中有菱形纹的正六边形的个数是( )| A. | 26 | B. | 31 | C. | 32 | D. | 36 |
19.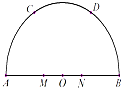 如图AB是半圆O的直径,C,D是弧$\widehat{AB}$的三等分点,M,N是线段AB的三等分点,若OA=6,则$\overrightarrow{MC}•\overrightarrow{ND}$=( )
如图AB是半圆O的直径,C,D是弧$\widehat{AB}$的三等分点,M,N是线段AB的三等分点,若OA=6,则$\overrightarrow{MC}•\overrightarrow{ND}$=( )
 如图AB是半圆O的直径,C,D是弧$\widehat{AB}$的三等分点,M,N是线段AB的三等分点,若OA=6,则$\overrightarrow{MC}•\overrightarrow{ND}$=( )
如图AB是半圆O的直径,C,D是弧$\widehat{AB}$的三等分点,M,N是线段AB的三等分点,若OA=6,则$\overrightarrow{MC}•\overrightarrow{ND}$=( )| A. | 18 | B. | 8 | C. | 26 | D. | 35 |
4.不等式1<|x+1|<3的解集中整数解的个数为( )
| A. | 3 | B. | 1 | C. | 4 | D. | 2 |