题目内容
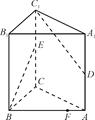
已知四棱锥 的底面是平行四边形,
的底面是平行四边形, ,
, ,
, 面
面 ,且
,且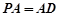 .若
.若 为
为 中点,
中点, 为线段
为线段 上的点,且
上的点,且 .
.
(1)求证: 平面
平面 ;
;
(2)求PC与平面PAD所成角的正弦值.
(1)证明过程详见解析(2) 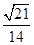
解析试题分析:
(1)本文利用面面垂直来证明线面垂直,即连接BD交AC于点O,取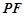 中点
中点 ,连接
,连接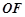 、
、 、
、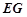 .利用
.利用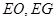 分别为
分别为 的中位线,说明它们对应平行,进而得到面
的中位线,说明它们对应平行,进而得到面 与面
与面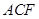 平行,再根据面面平行的性质得到线面平行.
平行,再根据面面平行的性质得到线面平行.
(2)要求线面角,需要找到线面角的代表角,即过C点做面PAD的垂线,因为PA垂直于底面,所以过C作线段AD的垂线与AD交于H,则CH垂直于面PAD,所以角CPH即为线面角的代表角,要求该角的正弦值,就需要求出PC与CH,可以利用三角形PAC和三角形ACH为直角三角形通过勾股定理求的.进而得到线面角的正弦值.
试题解析:
(1)证明:连接BD交AC于点O,
取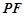 中点
中点 ,连接
,连接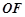 、
、 、
、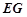 .
.
因为 、
、 分别是
分别是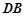 、
、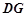 的中点,
的中点,
所以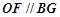 , 3分
, 3分
因为 、
、 分别是
分别是 、
、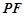 的中点,
的中点,
所以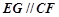 , 6分
, 6分
所以,平面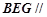 平面
平面 .
.
又因为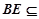 平面
平面 ,
,
故, 平面
平面 . 9分
. 9分
(2)因为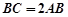 ,
, ,所以
,所以 .
.
过C作AD的垂线,垂足为H,则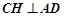 ,
,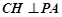 ,所以
,所以 平面PAD.
平面PAD.
故 为PC与平面PAD所成的角. 12分
为PC与平面PAD所成的角. 12分
设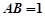 ,则
,则 ,
,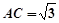 ,
, ,
,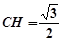
所以 ,即为所求. 15分
,即为所求. 15分
考点:面面平行 线面平行 线面夹角 勾股定理

练习册系列答案
相关题目
 中,
中, 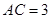 ,
,  ,
, ,点
,点 是
是 的中点.四面体
的中点.四面体 的体积是
的体积是 ,求异面直线
,求异面直线 与
与 所成的角.
所成的角.
 A1B1C1D1中,AD∥BC,AD⊥AB,AB=
A1B1C1D1中,AD∥BC,AD⊥AB,AB= ,AD=2,BC=4,AA1=2,E是DD1的中点,F是平面B1C1E与直线AA1的交点.
,AD=2,BC=4,AA1=2,E是DD1的中点,F是平面B1C1E与直线AA1的交点.
 A1B1C1,
A1B1C1,



 中,已知
中,已知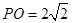 ,
,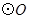 的直径
的直径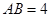 ,点
,点 在底面圆周上,且
在底面圆周上,且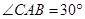 ,
,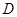 为
为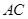 的中点.
的中点.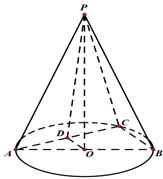
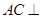 平面
平面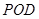 ;
;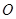 到面
到面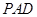 的距离.
的距离.