题目内容
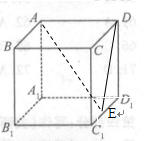
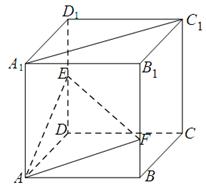
棱长为2的正方体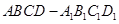 中,E为
中,E为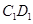 的中点.
的中点.
(1)求证: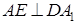 ;
;
(2)求异面直线AE与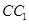 所成的角的正弦值.
所成的角的正弦值.
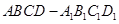 中,E为
中,E为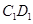 的中点.
的中点.
(1)求证:
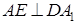 ;
;(2)求异面直线AE与
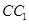 所成的角的正弦值.
所成的角的正弦值.(1)见解析(2)

试题分析:(1)可证
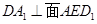 或
或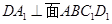 ,可证得
,可证得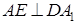 。(2)因为
。(2)因为 ∥
∥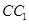 所以异面直线AE与
所以异面直线AE与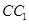 所成的角即为
所成的角即为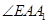 ,在
,在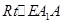 中可求得
中可求得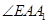 的正弦值。
的正弦值。试题解析:解:(1)在正方体
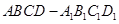 中,连接
中,连接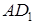 ,∴
,∴ 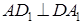 又∵
又∵ ∴
∴ ∴
∴ ∴
∴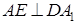 。(6分)
。(6分)(2)∵
 ∥
∥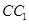 ∴异面直线AE与
∴异面直线AE与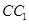 所成的角为
所成的角为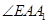 ,
,在
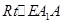 中,AE=3,
中,AE=3,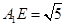 ,∴异面直线AE与
,∴异面直线AE与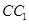 所成的角的正弦值为
所成的角的正弦值为 。(12分)
。(12分)
练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
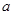 的正方体
的正方体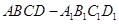 中,点
中,点 是棱
是棱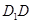 的中点,点
的中点,点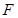 在棱
在棱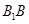 上,且满足
上,且满足 .
.
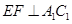 ;
;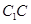 上确定一点
上确定一点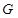 ,使
,使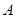 、
、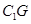 的长;
的长; 与平面
与平面 所成二面角的余弦值.
所成二面角的余弦值.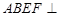 平面
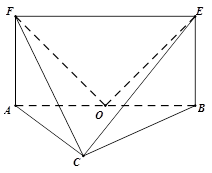
平面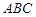 ,四边形
,四边形 为矩形,△
为矩形,△ 为
为 的中点,
的中点,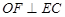 .
.
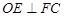 ;
; 的正切值.
的正切值.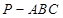 中,
中,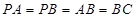 ,
,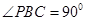 ,D为AC的中点,
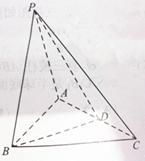
,D为AC的中点,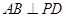 .
.
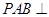 平面
平面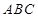 ;
;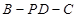 的余弦值.
的余弦值.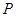 是正方体
是正方体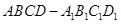 的棱
的棱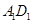 上的一个动点,设异面直线
上的一个动点,设异面直线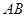 与
与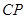 所成的角为
所成的角为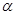 ,则
,则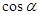 的最小值是 .
的最小值是 .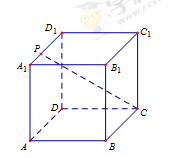
 中,与
中,与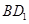 所在直线所成的角为
所在直线所成的角为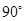 是( )
是( )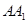
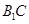
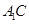
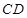
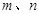 是两条不同的直线,
是两条不同的直线,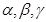 是三个不同的平面,给出下列四个命题:
是三个不同的平面,给出下列四个命题: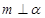 ,
,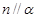 ,则
,则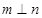
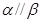 ,
,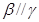 ,
,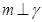
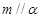 ,
,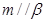 ,
,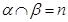 ,则
,则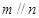
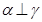 ,
,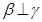 ,
,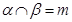 ,则
,则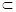 α,m
α,m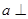 平面
平面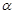 ,直线
,直线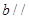 平面
平面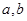 的位置关系是 .
的位置关系是 .