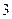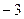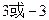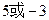题目内容
(本小题满分14分)如果对于函数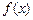 的定义域内任意的
的定义域内任意的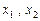 ,都有
,都有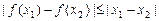 成立,那么就称函数
成立,那么就称函数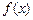 是定义域上的“平缓函数”.
是定义域上的“平缓函数”.
(1)判断函数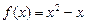 ,
,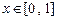 是否是“平缓函数”;(2)若函数
是否是“平缓函数”;(2)若函数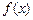 是闭区间
是闭区间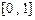 上的“平缓函数”,且
上的“平缓函数”,且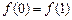 .证明:对于任意的
.证明:对于任意的
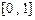 ,都有
,都有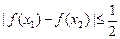 成立.(3)设
成立.(3)设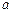 、
、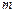 为实常数,
为实常数,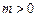 .若
.若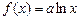 是区间
是区间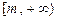 上的“平缓函数”,试估计
上的“平缓函数”,试估计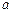 的取值范围(用
的取值范围(用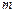 表示,不必证明).
表示,不必证明).
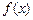 的定义域内任意的
的定义域内任意的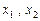 ,都有
,都有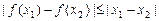 成立,那么就称函数
成立,那么就称函数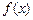 是定义域上的“平缓函数”.
是定义域上的“平缓函数”.(1)判断函数
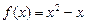 ,
,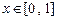 是否是“平缓函数”;(2)若函数
是否是“平缓函数”;(2)若函数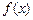 是闭区间
是闭区间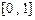 上的“平缓函数”,且
上的“平缓函数”,且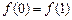 .证明:对于任意的
.证明:对于任意的
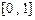 ,都有
,都有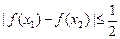 成立.(3)设
成立.(3)设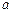 、
、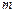 为实常数,
为实常数,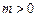 .若
.若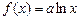 是区间
是区间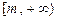 上的“平缓函数”,试估计
上的“平缓函数”,试估计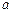 的取值范围(用
的取值范围(用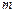 表示,不必证明).
表示,不必证明).(Ⅰ) 略 (Ⅱ) 略 (Ⅲ)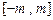
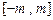
:(1)对于任意的
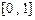 ,有
,有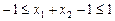 ,
, .2分
.2分
从而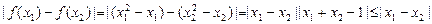 .
.
∴函数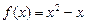 ,
,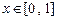 是“平缓函数”.……4分
是“平缓函数”.……4分
(2)当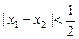 时,由已知得
时,由已知得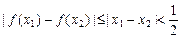 ;……………6分
;……………6分
当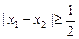 时,因为
时,因为
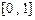 ,不妨设
,不妨设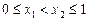 ,其中
,其中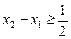 ,
,
因为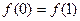 ,所以
,所以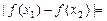
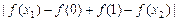
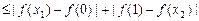
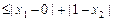
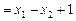
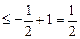 .
.
故对于任意的
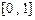 ,都有
,都有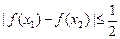 成立.……10分
成立.……10分
(3)结合函数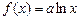 的图象性质及其在点
的图象性质及其在点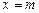 处的切线斜率,估计
处的切线斜率,估计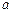 的取值范围是闭区间
的取值范围是闭区间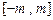 .……(注:只需直接给出正确结论)…………14分
.……(注:只需直接给出正确结论)…………14分

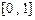 ,有
,有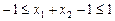 ,
, .2分
.2分从而
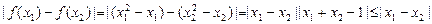 .
.∴函数
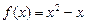 ,
,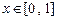 是“平缓函数”.……4分
是“平缓函数”.……4分(2)当
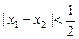 时,由已知得
时,由已知得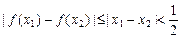 ;……………6分
;……………6分当
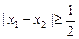 时,因为
时,因为
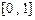 ,不妨设
,不妨设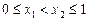 ,其中
,其中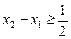 ,
,因为
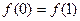 ,所以
,所以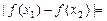
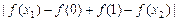
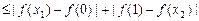
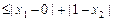
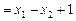
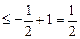 .
.故对于任意的

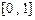 ,都有
,都有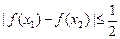 成立.……10分
成立.……10分(3)结合函数
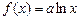 的图象性质及其在点
的图象性质及其在点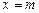 处的切线斜率,估计
处的切线斜率,估计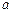 的取值范围是闭区间
的取值范围是闭区间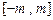 .……(注:只需直接给出正确结论)…………14分
.……(注:只需直接给出正确结论)…………14分
练习册系列答案
相关题目
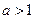 ,函数
,函数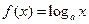 在区间
在区间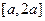 上的最大值与最小值之差为
上的最大值与最小值之差为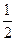 ,则
,则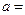
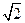
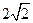
 ,g(x)=
,g(x)= 的图象的示意图如图所示,
的图象的示意图如图所示, )B(
)B(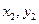 ),且
),且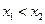
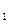 ,C
,C 分别对应哪一个函数?
分别对应哪一个函数? 且
且 ,指出a,b的值,并说明理由;
,指出a,b的值,并说明理由; 1
1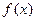 ,若存在
,若存在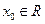 ,使
,使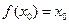 成立,则称
成立,则称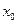 为
为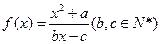 有且仅有两个不动点
有且仅有两个不动点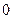 、
、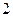 ,且
,且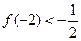 。
。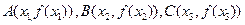 从左到右依次是函数
从左到右依次是函数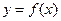 图象上三点,其中
图象上三点,其中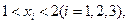 求证:⊿
求证:⊿ 是钝角三角形.
是钝角三角形. 对于任意实数
对于任意实数 满足条件
满足条件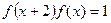 ,若
,若 则
则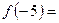 __________
__________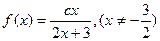 满足
满足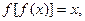 则常数
则常数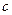 等于( )
等于( )