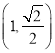题目内容
【题目】已知抛物线![]() ,过点
,过点![]() 的动直线
的动直线![]() 与
与![]() 相交于
相交于![]() 两点,抛物线
两点,抛物线![]() 在点
在点![]() 和点
和点![]() 处的切线相交于点
处的切线相交于点![]() .
.
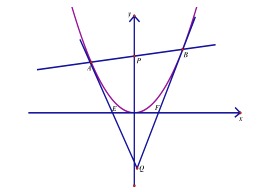
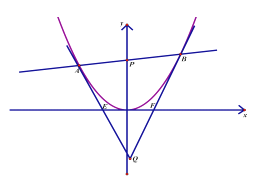
(Ⅰ)写出抛物线的焦点坐标和准线方程;
(Ⅱ)求证:点![]() 在直线
在直线![]() 上;
上;
【答案】(Ⅰ)![]() ,
, ![]() (Ⅱ)见解析.
(Ⅱ)见解析.
【解析】试题分析:(Ⅰ)根据标准方程可以直接写出抛物线的焦点坐标和准线方程,注意焦点在![]() 轴上.(Ⅱ)又
轴上.(Ⅱ)又![]() 为两条切线的交点,故可以求出两条切线方程(它们与切点的横坐标有关),联立它们可以得到
为两条切线的交点,故可以求出两条切线方程(它们与切点的横坐标有关),联立它们可以得到![]() 的坐标.最后利用动直线
的坐标.最后利用动直线![]() 过定点
过定点![]() 可以得到两个切点横坐标的关系,从而得到
可以得到两个切点横坐标的关系,从而得到![]() 的纵坐标为定值.
的纵坐标为定值.
解析:(Ⅰ)解:焦点坐标为![]() ,准线方程为
,准线方程为![]() .
.
(Ⅱ)证明:由题意,知直线![]() 的斜率存在,故设
的斜率存在,故设![]() 的方程为
的方程为![]() ,由方程组
,由方程组![]() ,得
,得![]() .由题意得
.由题意得![]() .设
.设![]() ,则
,则![]() .又
.又![]() ,所以抛物线在点
,所以抛物线在点![]() 处的切线的斜率为
处的切线的斜率为![]() ,抛物线在点
,抛物线在点![]() 处的切线方程为
处的切线方程为![]() ,化简得
,化简得![]() , ①.同理,抛物线在点
, ①.同理,抛物线在点![]() 处的切线方程为
处的切线方程为![]() ②,联立方程①②,得
②,联立方程①②,得![]() 即
即![]() ,因为
,因为![]() ,所以
,所以![]() ,代入①,得
,代入①,得![]() ,所以点
,所以点![]() ,即
,即![]()
所以点![]() 在直线
在直线![]() 上.
上.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目