题目内容
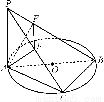
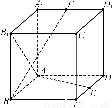
如图,在四棱锥PABCD中,PD⊥底面ABCD,AD⊥AB,CD∥AB,AB=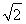 AD=2,CD=3,直线PA与底面ABCD所成角为60°,点M、N分别是PA、PB的中点.求证:
AD=2,CD=3,直线PA与底面ABCD所成角为60°,点M、N分别是PA、PB的中点.求证:
(1)MN∥平面PCD;
(2)四边形MNCD是直角梯形;
(3)DN⊥平面PCB.
(1)见解析(2)见解析(3)见解析
【解析】(1)因为点M、N分别是PA、PB的中点,所以MN∥AB.
因为CD∥AB,所以MN∥CD.
又CD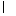 平面PCD,MN
平面PCD,MN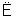 平面PCD,所以MN∥平面PCD.
平面PCD,所以MN∥平面PCD.
(2)因为AD⊥AB,CD∥AB,所以CD⊥AD.
因为PD⊥底面ABCD,CD?平面ABCD,
所以CD⊥PD.
因为AD∩PD=D,所以CD⊥平面PAD.
因为MD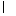 平面PAD,所以CD⊥MD.
平面PAD,所以CD⊥MD.
又MN∥CD,MN≠CD,
所以四边形MNCD是直角梯形.
(3)因为PD⊥底面ABCD,所以∠PAD就是直线PA与底面ABCD所成的角,
从而∠PAD=60°.
在Rt△PDA中,AD=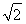 ,PD=
,PD=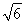 ,PA=2
,PA=2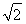 ,MD=
,MD=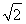 .
.
在直角梯形MNCD中,MN=1,ND=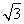 ,CD=3,CN=
,CD=3,CN=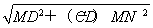 =
=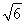 ,
,
从而DN2+CN2=CD2,所以DN⊥CN.
在Rt△PDB中,PD=DB=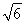 ,N是PB的中点,则DN⊥PB.
,N是PB的中点,则DN⊥PB.
又PB∩CN=N,所以DN⊥平面PCB.

练习册系列答案
相关题目