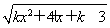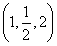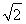题目内容
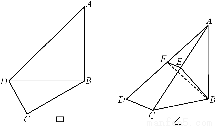
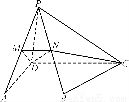
如图所示,四棱锥PABCD中,PA⊥底面ABCD,BC=CD=2,AC=4,∠ACB=∠ACD=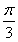 ,F为PC的中点,AF⊥PB.
,F为PC的中点,AF⊥PB.
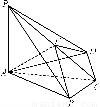
(1)求PA的长;
(2)求二面角B-AF-D的正弦值.
(1)2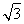 (2)
(2)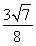
【解析】(1)如图,连结BD交AC于O,因为BC=CD,即△BCD为等腰三角形,又AC平分∠BCD,
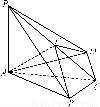
故AC⊥BD.以O为坐标原点,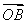 、
、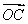 、
、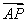 的方向分别为x轴、y轴、z轴的正方向,建立空间直角坐标系Oxyz,则OC=CDcos
的方向分别为x轴、y轴、z轴的正方向,建立空间直角坐标系Oxyz,则OC=CDcos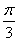 =1,而AC=4,得AO=AC-OC=3.又OD=CDsin
=1,而AC=4,得AO=AC-OC=3.又OD=CDsin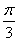 =
=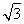 ,故A(0,-3,0),B(
,故A(0,-3,0),B(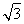 ,0,0),C(0,1,0),D(-
,0,0),C(0,1,0),D(-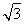 ,0,0).
,0,0).
因为PA⊥底面ABCD,可设P(0,-3,z),由F为PC边中点,得F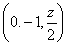 ,又
,又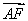 =
=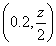 ,
,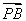 =(
=(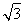 ,3,-z),因AF⊥PB,故
,3,-z),因AF⊥PB,故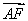 ·
·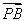 =0,即6-
=0,即6-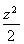 =0,z=2
=0,z=2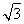 (舍去-2
(舍去-2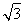 ),所以|
),所以|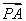 |=2
|=2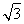 .
.
(2)由(1)知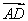 =(-
=(-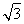 ,3,0),
,3,0),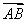 =(
=(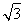 ,3,0),
,3,0),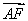 =(0,2,
=(0,2,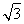 ).设平面FAD的法向量为n1=(x1,y1,z1),平面FAB的法向量为n2=(x2,y2,z2).
).设平面FAD的法向量为n1=(x1,y1,z1),平面FAB的法向量为n2=(x2,y2,z2).
由n1·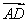 =0,n1·
=0,n1· =0,得
=0,得 因此可取n1=(3,
因此可取n1=(3,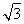 ,-2).
,-2).
由n2·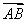 =0,n2·
=0,n2·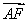 =0,得
=0,得 故可取n2=(3,-
故可取n2=(3,-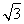 ,2).
,2).
从而向量n1,n2的夹角的余弦值为cos〈n1,n2〉=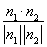 =
=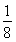 .
.
故二面角B-AF-D的正弦值为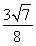 .
.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目