题目内容
已知数列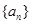 是递增数列,且满足
是递增数列,且满足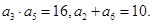
(Ⅰ)若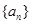 是等差数列,求数列
是等差数列,求数列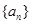 的通项公式;
的通项公式;
(Ⅱ)对于(Ⅰ)中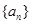 ,令
,令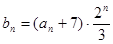 ,求数列
,求数列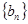 的前
的前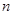 项和
项和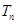 .
.
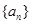 是递增数列,且满足
是递增数列,且满足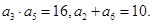
(Ⅰ)若
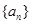 是等差数列,求数列
是等差数列,求数列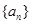 的通项公式;
的通项公式;(Ⅱ)对于(Ⅰ)中
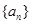 ,令
,令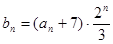 ,求数列
,求数列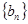 的前
的前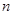 项和
项和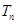 .
.(Ⅰ)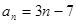 (Ⅱ)
(Ⅱ)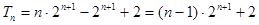
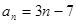 (Ⅱ)
(Ⅱ)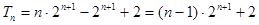
本试题主要是考查了数列的通项公式的求解以及数列求和的综合运用。
(1)根据题意设出首项和公差,代入已知关系式中得到通项公式。
(2)在第一问可知数列的通项公式,然后分析运用错位相减法得到结论。
解:(1)根据题意: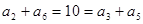 ,又
,又 ,所以
,所以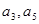 是方程
是方程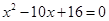 的两根,且
的两根,且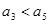 ,解得
,解得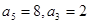 ,所以
,所以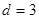 ,
, 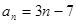 . ……………………………5分
. ……………………………5分
(2)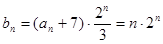 ,则
,则
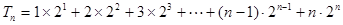 ①
①
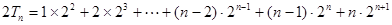 ②,
②,
得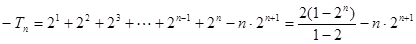 ,
,
所以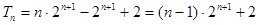 .………………………12分
.………………………12分
(1)根据题意设出首项和公差,代入已知关系式中得到通项公式。
(2)在第一问可知数列的通项公式,然后分析运用错位相减法得到结论。
解:(1)根据题意:
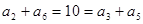 ,又
,又 ,所以
,所以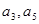 是方程
是方程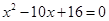 的两根,且
的两根,且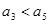 ,解得
,解得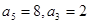 ,所以
,所以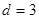 ,
, 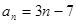 . ……………………………5分
. ……………………………5分(2)
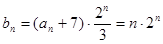 ,则
,则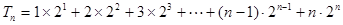 ①
①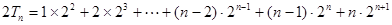 ②,
②,得
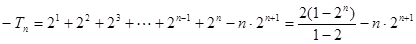 ,
,所以
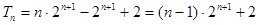 .………………………12分
.………………………12分 
练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
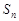 是等差数列
是等差数列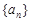 的前
的前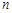 项和,若
项和,若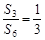 ,则
,则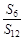 等于( )
等于( )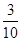
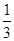
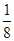
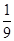
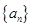 满足
满足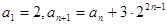 ,
,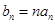 ,求数列的前n项和
,求数列的前n项和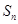 .
.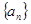 中,
中,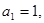 且点
且点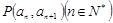 在直线
在直线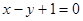 上.
上.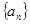 的通项公式;
的通项公式; (2)若函数
(2)若函数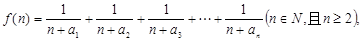 求函数
求函数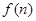 的最小值;
的最小值;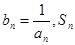 表示数列
表示数列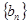 的前
的前 项和.试问:是否存在关于
项和.试问:是否存在关于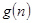 ,使得
,使得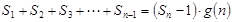 对于一切不小于2的自然数
对于一切不小于2的自然数 ,求数列{bn}的前
,求数列{bn}的前 项和Sn.
项和Sn. 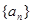 中,
中,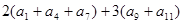 =24,则数列的前13项和等于
=24,则数列的前13项和等于 
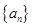 的首项为
的首项为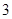 ,
,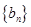 为等差数列且
为等差数列且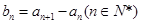 .若则
.若则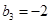 ,
,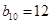 ,则
,则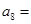 ( )
( )